Spring Hardening
Isotropic, kinematic or uncoupled spring hardening options can be defined by the hardening flag .
These examples only include the spring stiffness without any damping.
Linear Elastic Spring, H=0

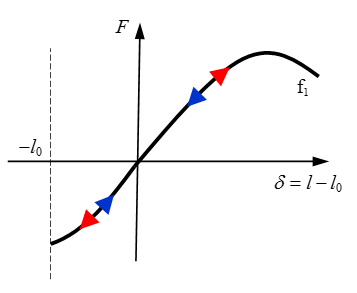
Nonlinear Elastic Spring, H=0
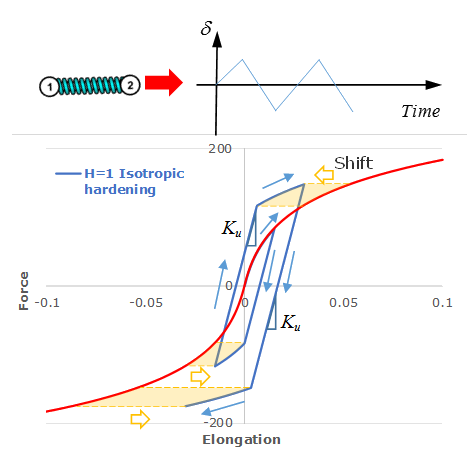
Nonlinear Elastic Plastic Spring with Isotropic Hardening, H=1
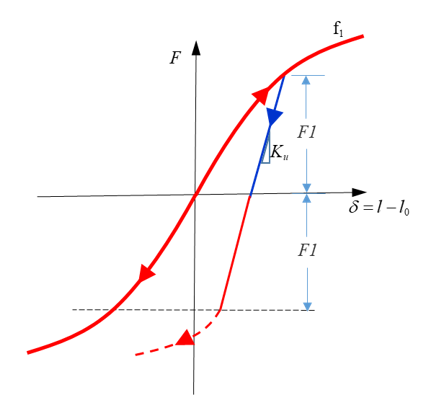
Nonlinear Elastic Plastic Spring with Uncoupled Hardening, H=2

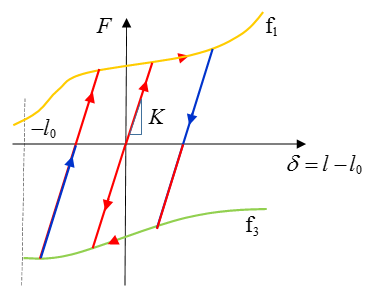
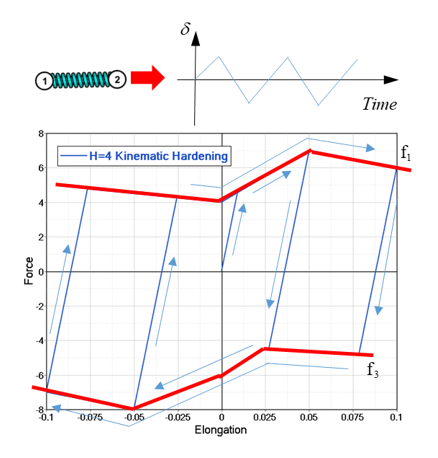
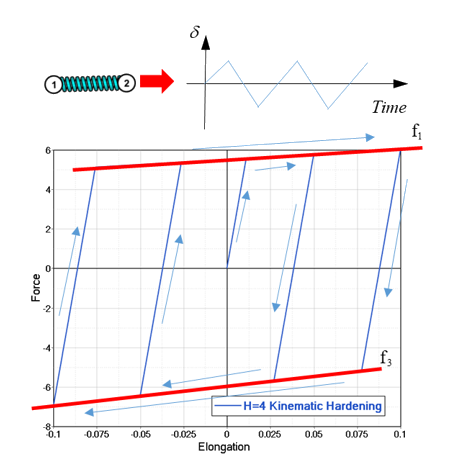
Nonlinear Elastic Plastic Spring with Kinematic Hardening, H=4
Nonlinear Elastic Plastic Spring Nonlinear Unloading, H=5
When =5, uncoupled hardening in compression and tensile with nonlinear unloading is modeled.
Function defines the residual displacement related to displacement; where the unloading starts at . The unloading is defined by:
with,
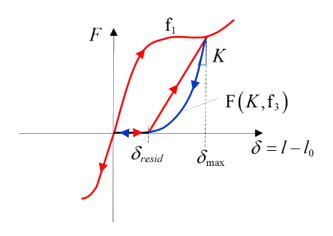

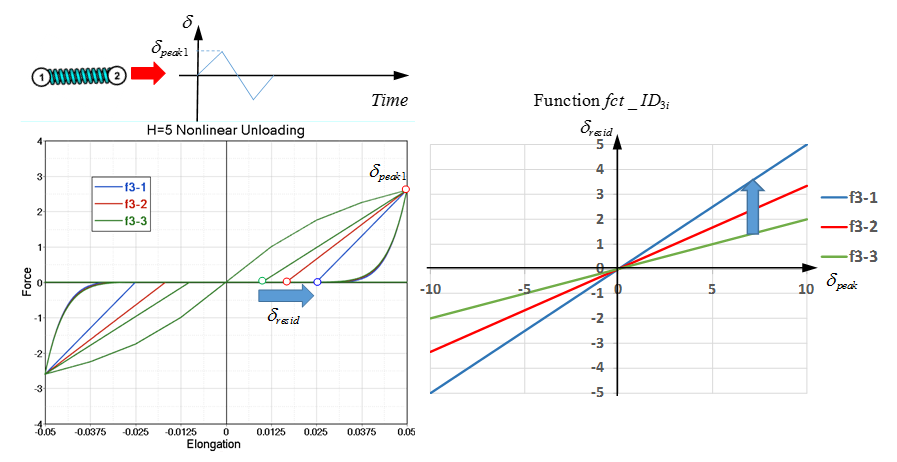
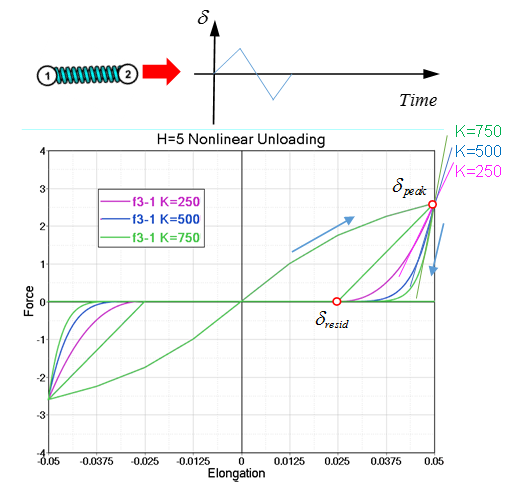
Comparing Figure 10 and Figure 11, shows that the function only effects the residual displacement and the shape of unloading curve. The shape of unloading curve is controlled by stiffness and (unloading start displacement).
If the same stiffness and same are used, then the unloading curve has the same shape.
If the same stiffness but different are used, then the unloading curve has a different shape.
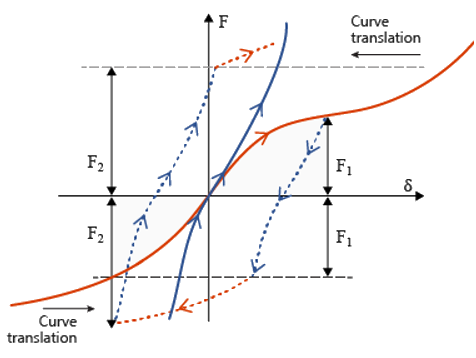
Nonlinear Elastic Plastic Spring Isotropic Hardening and Nonlinear Unloading, H=6
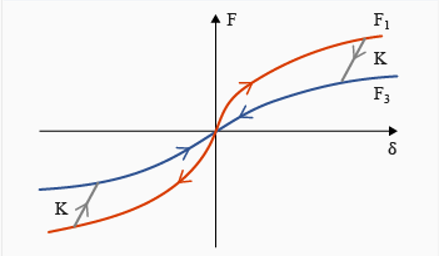
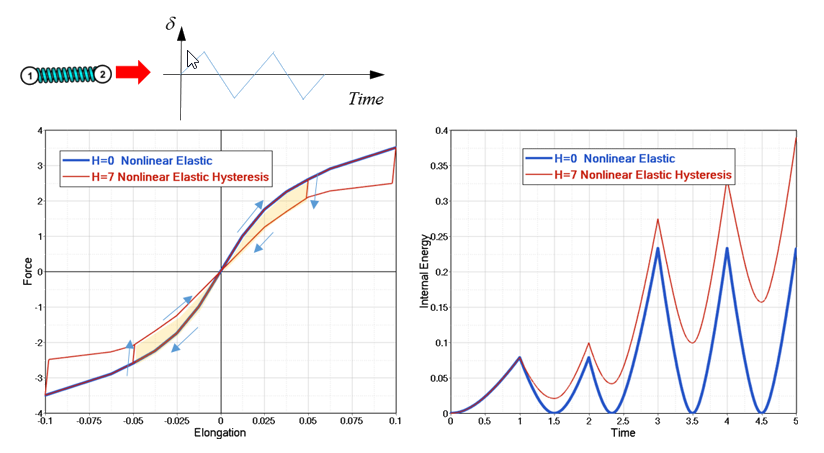
Nonlinear Elastic Plastic Spring Elastic Hysteresis, H=7
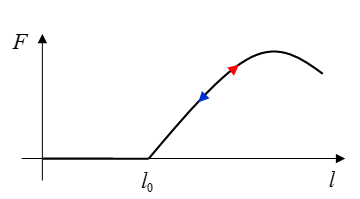
Nonlinear Elastic Total Length Function, H=8

Dashpot
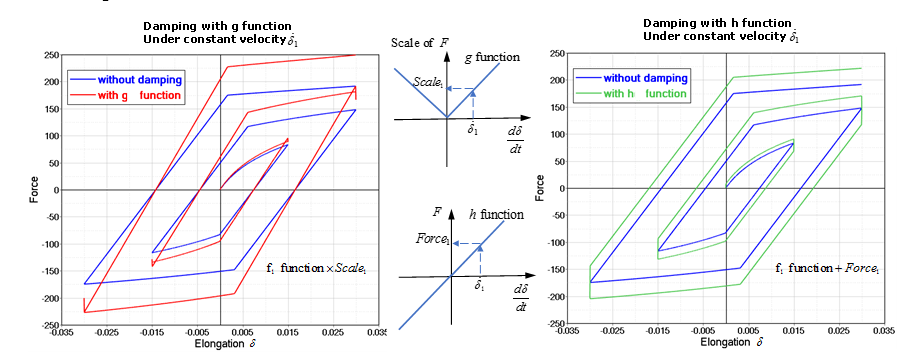
Damping Using a Function
Remembering that the function scales the force are , whereas the function adds to the force . Figure 19 compares these two different methods.
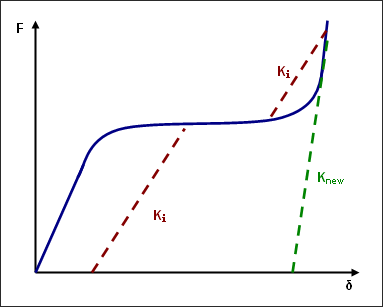
Inconsistent Stiffness
WARNING ID: 506 ** WARNING IN SPRING PROPERTY ** WARNING IN SPRING PROPERTY SET ID=XXX STIFFNESS VALUE 100 IS NOT CONSISTENT WITH THE MAXIMUM SLOPE (4550) OF THE YIELD FUNCTION ID=X THE STIFFNESS VALUE IS CHANGED TO 1000