Stress-Strain Computation Options (/PROP)

Usually a small stress formulation is used to simulate problems for small deformations. Typical application covers linear elastic studies. For nonlinear problems with elasto-plastic behavior and large deformation, it is recommended to use a large strain and large displacement formulation.

For some problems with very large mesh distortion, a large strain formulation has some limitations. If the time step decreases too much, the CPU time will increase highly and if a brick element reaches a negative volume, the computation will stop, or this element may have to be removed.

With a small strain formulation these limitations disappear; however, it seems surprising to use a small strain formulation in case of large deformation; but this can be a better solution than element deletion. For specific materials, like honeycomb, for which there is no Poisson's effect, the small strain limitation can be corrected just by using the appropriated stress strain curve.

Large Strain Formulation

By default, Radioss uses a large strain, large displacement formulation with explicit time integration. By computing the derivative of shape functions at each cycle, large displacement formulation is obtained. The large strain formulation results from incremental strain computation. Stresses and strains are therefore true stresses and true strains.

Time integration of Cauchy stress (true stress) can be performed as:

σ_{i j} (t + δ t) = σ_{i j} (t) + \frac{d σ_{i j} (t)}{d t} d t

The objectivity of stress rate means that the stress tensor follows the rigid body rotation of the material. Stress rate is the function of element average rigid body rotation and of strain rate. Stability of explicit scheme is given by Courant condition:

Δ t < \frac{l}{c}

With $l$ being the element characteristic length and $c$ is the sound speed. The time step is computed at each cycle. Large element deformation can provide a large time step decrease. For very large deformations, a negative volume can be reached and then becomes impossible to integrate the stresses over the volume.

Small Strain Formulation

Assuming a constant Jacobian matrix during time and also a constant volume, previous equations degenerate into a small strain formulation. All special variables are then values defined at time t=0 (or at the time the small strain formulation is initiated).

Time step then becomes constant:

Δ t = \frac{l_{0}}{c}

Then the effective negative volume has no effect on the computation (only the initial volume is used), but the small strain assumption is acceptable for some specific material behavior, like honeycomb; so the small displacement formulation is obviously not recommended for crash analysis.

For stress objectivity, the Jacobian matrix time transformation depends upon the element deformation and the element rigid body rotation. Rigid body translation has no effect on the Jacobian matrix. If element deformation is not taken into account, a small strain formulation is obtained. If element rigid body rotation is not taken into account, a small displacement formulation is obtained.

To switch to a small strain formulation after reaching $Δ T_{\min}$ , the following options can be used in the Engine file:

/DT/BRICK/CST

$Δ T_{s c a}$ $Δ T_{\min}$

/DT/SHELL/CST

$Δ T_{s c a}$ $Δ T_{\min}$

/DT/SH_3N/CST

$Δ T_{s c a}$ $Δ T_{\min}$

Note: For some brick material laws, the sound speed is pressure dependent. Therefore, it possible that time step becomes slightly smaller than

Δ T_{\min}

.

Update Stress and Strains (/PROP)

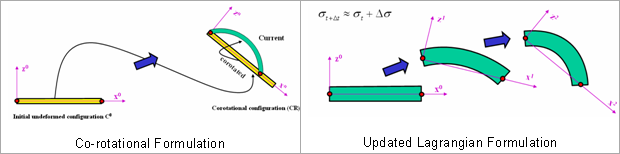
In Radioss two formulations are available (Figure 1):

Co-rotational Formulation (CR): The FEM equations of each element are referred to two systems. A fixed or base configuration is used to compute the rigid body motion of the element. Then, the deformed current state is referred to the co-rotated configuration, which is obtained by the rigid body motion of the initial reference.
Updated Lagrangian Formulation (ULF): The reference is the last known (accepted) solution. It remains fixed over a step and updated at the end of each step.

The co-rotational formulation is the most recent of the formulations in geometrically Nonlinear Structural Analysis. It decouples small strain material nonlinearities from geometric nonlinearities and naturally handles the question of frame indifference of anisotropic behavior, due to material nonlinearities. For historical Radioss solid elements, the co-rotational formulation is optional and should be activated before the computations (refer to /PROP/SOLID).

Note: An updated Lagrangian formulation can handle incorrect results for solids in large shear deformation, due to the accumulation of updating errors at each cycle. The use of co-rotational formulation is strongly recommended, especially when elements undergo large shear deformation or large rigid body motions.