/MONVOL/COMMU (Obsolete)
Block Format Keyword Describes the airbag with communications monitored volume type.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MONVOL/COMMU/monvol_ID/unit_ID | |||||||||
| monvol_title | |||||||||
| surf_IDex | |||||||||
| Ascalet | AscaleP | AscaleS | AscaleA | AscaleD | |||||
| Pext | T0 | Iequi | Ittf | ||||||
| cpai | cpbi | cpci | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Njet |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| cpa | cpb | cpc | |||||||
| fct_IDmas | Iflow | Fscalemas | fct_IDT | FscaleT | sens_ID | ||||
| Ijet | node_ID1 | node_ID2 | node_ID3 | ||||||
| fct_IDPt | fct_IDP | fct_IDP | FscalePt | FscaleP | FscaleP | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Nvent |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| surf_IDv | Avent | Bvent | Tstop | ||||||
| Tvent | fct_IDV | FscaleV | IdtPdef | ||||||
| fct_IDt | fct_IDP | fct_IDA | Fscalet | FscaleP | FscaleA | ||||
| fct_IDt' | fct_IDP' | fct_IDA' | Fscalet' | FscaleP' | FscaleA' | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Nbag |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| bag_ID | surf_IDc | Acom | Tcom | ||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| monvol_ID | Monitored volume
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| monvol_title | Monitored volume
title. (Character, maximum 100 characters) |
|
| surf_IDex | External surface
identifier. 1 (Integer) |
|
| Ascalet | Abscissa scale factor for
time based functions. Default = 1.0 (Real) |
|
| AscaleP | Abscissa scale factor for
pressure based functions. Default = 1.0 (Real) |
|
| AscaleS | Abscissa scale factor for
area based functions. Default = 1.0 (Real) |
|
| AscaleA | Abscissa scale factor for
angle based functions. Default = 1.0 (Real) |
|
| AscaleD | Abscissa scale factor for
distance based functions. Default = 1.0 (Real) |
|
| Volumetric
viscosity. Default = 0.01 (Real) |
||
| Pext | External
pressure. (Real) |
|
| T0 | Initial
temperature. Default = 295 (Real) |
|
| Iequi | Initial thermodynamic
equilibrium flag.
(Integer) |
|
| Ittf | Venting time shift flag.
Active only when injection sensor is specified.
|
|
| Ratio of specific heats at
initial temperature.
(Real) |
||
| cpai | cpa
coefficient in the relation
cpi(T) (Real) |
|
| cpbi | cpb
coefficient in the relation
cpi(T). (Real) |
|
| cpci | cpc
coefficient in the relation
cpi(T). (Real) |
|
| Njet | Number of
injectors. (Integer) |
|
| Nvent | Number of vent
holes. (Integer) |
|
| surf_IDv | Vent holes membrane
surface identifier. 17 (Integer) |
|
| Avent | If
surf_IDv ≠
0: scale factor on surface. Default = 1.0 If surf_IDv = 0: surface of vent holes. Default = 0.0 (Real) |
, if surf_IDV = 0 |
| Bvent | If
surf_IDv ≠
0: scale factor on impacted surface. Default = 1.0 If surf_IDv = 0: Bvent is reset to 0. Default = 0.0 (Real) |
, if surf_IDV = 0 |
| Tvent | Start time for
venting. Default = 0.0 (Real) |
|
| Tstop | Stop time for
venting. Default = 1E+30 (Real) |
|
| fct_IDT | Porosity versus time
function identifier. (Integer) |
|
| fct_IDP | Porosity versus pressure
function identifier. (Integer) |
|
| fct_IDA | Porosity versus area
function identifier. (Integer) |
|
| FscaleT | Scale factor for
fct_IDT. Default = 1.0 (Real) |
|
| FscaleP | Scale factor for
fct_IDP. Default = 1.0 (Real) |
|
| FscaleA | Scale factor for
fct_IDA. Default = 1.0 (Real) |
|
| γ | Ratio of specific heats.
(Real) |
|
| cpa | cpa
coefficient in the relation cp(T) (Real) |
|
| cpb | cpb
coefficient in the relation cp(T). (Real) |
|
| cpc | cpc
coefficient in the relation cp(T). (Real) |
|
| fct_IDmas | Mass of injected gas
versus time function identifier. (Integer) |
|
| Iflow | Mass versus time function
input type flag.
(Integer) |
|
| Fscalemas | Mass function scale
factor. Default = 1.0 (Real) |
|
| fct_IDT | Temperature of injected
gas versus time function identifier. (Integer) |
|
| FscaleT | Temperature function scale
factor. Default = 1.0 (Real) |
|
| sens_ID | Sensor identifier to start
injections. (Integer) |
|
| Ijet | Jetting flag.
(Integer) |
|
| node_ID1, node_ID2, node_ID3 | Node identifiers
N1,
N2, and
N3 for jet shape
definition. (Integer) |
|
| fct_IDPt | Identifier of the function
number defining
. (Integer) |
|
| fct_IDP | Identifier of the function
number defining
. (Integer) |
|
| fct_IDP | Identifier of the function
number defining
. (Integer) |
|
| FscalePt | Scale factor for
fct_IDPt. Default = 1.0 (Real) |
|
| FscaleP | Scale factor for
fct_IDP
. Default = 1.0 (Real) |
|
| FscaleP | Scale factor for
fct_IDP
. Default = 1.0 (Real) |
|
| Minimum duration pressure
exceeds Pdef to
open vent hole membrane. (Real) |
||
| fct_IDV | Outflow velocity function
identifier. (Integer) |
|
| FscaleV | Scale factor on
fct_IDV. Default = 1.0 (Real) |
|
| IdtPdef | Time delay flag when
is reached:
|
|
| fct_IDt' | Porosity versus time when
contact function identifier. (Integer) |
|
| fct_IDP' | Porosity versus pressure
when contact function identifier. (Integer) |
|
| fct_IDA' | Porosity versus impacted
surface function identifier. (Integer) |
|
| Fscalet' | Scale factor for
fct_IDt'. Default = 1.0 (Real) |
|
| FscaleP' | Scale factor for
fct_IDP'. Default = 1.0 (Real) |
|
| FscaleA' | Scale factor for
fct_IDA'. Default = 1.0 (Real) |
|
| Nbag | Number of communicating
airbags. (Integer) |
|
| bag_ID | Airbag identifier. 26 (Integer) |
|
| surf_IDc | Communicating surface
identifier. (Integer) |
|
| Pressure difference to
open communication surface membrane. (Real) |
||
| Acom | Communication surface
coefficient. Default = 1.0 (Real) |
|
| Tcom | Start time for
communication. (Real) |
|
| Minimum duration pressure
difference exceeds
to open communication surface
membrane. (Real) |
Comments
- surf_IDex must be defined using segments associated with 4-nodes or 3-nodes shell elements (possibly void elements).
- The volume must be closed and the normals must be oriented outwards.
- Abscissa scale factors
are used to transform abscissa units in airbag functions, for
example:
(1) Where, t is the time.(2) Where, p is the pressure.
- The initial pressure is set to Pext.
- The gas within each communicating chamber should have the same characteristics: and cp.
- Initial thermodynamic
equilibrium is written at time zero
(Iequi =0)
or at beginning of jetting (Iequi
=1), based on the following equation with respect to the volume
at time zero, or the volume at beginning of jetting:
(3) Where, M0 is the mass of gas initially filling the airbag, Mi is the molar mass of the gas initially filling the airbag, and R is the gas constant depending on the units system.(4) - Ratio of specific heats
at constant pressure per mass unit
cpi of the gas initially
filling the airbag is quadratic versus temperature:
(5) - Gas constant at initial
temperature
must be related to specific heat per mass unit at initial
temperature and molar mass of the gas initially filling the airbag with respect to
the following relation:
(6) Where, Mi is the molar mass of the gas initially filling the airbag and R is the gas constant depending on the units system.(7) - The characteristics of the gas initially filling the airbag must be defined (no default) and must be equal for each communicating airbag.
- Ratio of specifics at
constant pressure per mass unit cpi
of the gas is quadratic with regard to the temperature:
(8) - Gas constant at initial
temperature
must be related to specific heat per mass unit at initial
temperature and molar mass of the with respect to the following
relation:
(9) Where, M is the molar mass of the gas and R is the gas constant depending on the units system.(10) - If jetting is used, an
additional
Pjet pressure is applied to
each element of the airbag:
(11) - With
being the normalized vector between the
projection of the center of the element upon segment (node_ID1 and node_ID3) and the center of the
element;
the angle between vectors
MN2 and
(in degrees),
the distance between the center of the element and its
projection upon segment (node_ID1 and node_ID3).The projection of a point upon segment (node_ID1 and node_ID3) is defined as the projection of the point in direction MN2upon the line (node_ID1and node_ID3) if it lies inside the segment (node_ID1 and node_ID3). If this is not the case, the projection of the point upon segment (node_ID1 and node_ID3) is defined as the closest node node_ID1 or node_ID3.
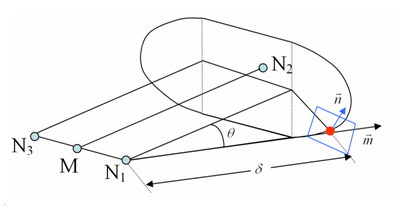
Figure 1. Dihedral Shape of the Jetwith M between of N1and N3
- If node_ID3= 0, node_ID3 is set to node_ID1 and the dihedral shape is reduced to a conical shape.
- Vent hole membrane is deflated if T > Tvent or if the pressure exceeds Pdef during more than .
- If
fct_IDV = 0:
isenthalpic outflow is assumed, else Chemkin model is used and outflow velocity
is:
(12) - Isenthalpic model
Venting or the expulsion of gas from the volume, is assumed to be isenthalpic.
The flow is also assumed to be unshocked, coming from a large reservoir and through a small orifice with effective surface area, A.
Conservation of enthalpy leads to velocity, u at the vent hole. The Bernouilli equation is then written as:
(monitored volume) (vent hole)
Applying the adiabatic conditions:
(monitored volume) (vent hole)
Where, P is the pressure of gas into the airbag and is the density of gas into the airbag.
Therefore, the exit velocity is given by:(13) For supersonic flows the outlet velocity is determined as described in 10.4.4.1 of the Theory Manual.
The mass out flow rate is given by:(14) The energy flow rate is given by:(15) Where, V is the airbag volume and E is the internal energy of gas into the airbag.
- Chemkin model
(16) Where, is the density of the gas within the airbag.
- Isenthalpic model
- If
surf_IDv ≠ 0
(surf_IDv is defined).
(17) Where, A is the Area of surface surf_ID.
- If
surf_IDv = 0
(surf_IDv is not
defined).
(18) - Functions fct_IDt and fct_IDP are assumed to be equal to 1, if they are not specified (null identifier).
- Function fct_IDA is assumed as the fct_IDA(A) = A, if it is not specified.
- In order to use porosity during contact, flag IBAG must be set to 1 in the interfaces concerned (Line 3 of interface Type 5 and Type 7). If not, the nodes impacted into the interface are not considered as impacted nodes in the previous formula for Aimpacted and Anon_impacted.
- Vent holes surface is
computed as follows:If surf_IDv = 0 (surf_IDv is not defined).
(19) - If
surf_IDv ≠ 0
(surf_IDv is defined).
(20) with impacted surface:(21) and non-impacted surface:(22) Where for each element e of the vent holes surf_IDv, nc(e) means the number of impacted nodes among the n(e) nodes defining the element.
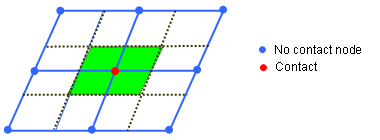
Figure 2. From Nodes Contact to Impacted/Non-impacted Surface - Functions fct_IDt' and fct_IDP' are assumed to be equal to 1, if they are not specified (null identifier).
- Function fct_IDA' is assumed as the fct_IDA'(A) = A, if it is not specified.
- All communicating airbags bag_ID should be type COMMU monitored volumes.
- Only the communication from the monitored volume monvol_ID to airbag bag_ID is considered (outwards communication).
- When defining venting,
there are some limitations concerning the definition of airbag surface and surface
venting:
- The airbag external surface should be built only from shells and 3-nodes shell elements.
- The airbag external surface can not be defined with option /SURF/SEG (nor with option /SURF/SURF if a sub-surface is defined with option /SURF/SEG).
- Same restriction applies to vent hole surface.
- Shells and 3-nodes shell elements included in vent hole surface have to be included also in external surface.
- Shells and 3-nodes shell elements included in communicating surface have to also be included in external surface.
- Communication surface is open if T > Tvent or if the pressure exceeds during more than .