Ityp = 3

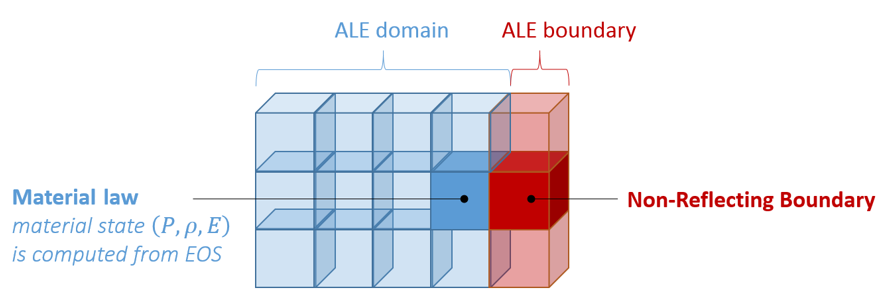
Block Format Keyword This law enables to model a non-reflecting boundary (NRF). Input card is similar to /MAT/LAW11 (BOUND), but introduces two new lines to define turbulence parameters.

Format


(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
/MAT/B-K-EPS/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$		$ρ_{0}$
`Ityp`		`P`_sh

Ityp =3: Non-Reflecting Boundary


(1)	(3)	(5)	(6)	(7)
	`c`	$l_{c}$
Blank Format
Blank Format
Blank Format
$ρ_{0} κ_{0}$	$ρ_{0} ε_{0}$	`fct_ID`_k	`fct_ID`_e
$C_{μ}$	$σ_{κ}$	$σ_{ε}$		$P_{r} / P_{r t}$
Blank Format

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. 3 (Real)	$[\frac{kg}{m^{3}}]$
$ρ_{0}$	Reference density used in E.O.S (equation of state). Default $ρ_{0} = ρ_{i}$ (Real)	$[\frac{kg}{m^{3}}]$
`Ityp`	Boundary condition type. 1 = 0 Gas inlet (from stagnation point data) = 1 Liquid inlet (from stagnation point data) = 2 General inlet/outlet = 3 Non-reflecting boundary (Integer)
`P`_sh	Pressure shift. 2 (Real)	$[Pa]$
`c`	Outlet sound speed. 1 (Real)	$[\frac{m}{s}]$
$l_{c}$	Characteristic length. 1 (Real)	$[m^{3}]$
$ρ_{0} κ_{0}$	Initial turbulent energy. (Real)	$[J]$
$ρ_{0} ε_{0}$	Initial turbulent dissipation. (Real)	$[J]$
`fct_ID`_k	Function $f_{κ} (t)$ identifier for turbulence modeling. = 0 $κ = κ_{adjacent}$ > 0 $κ = κ_{0} \cdot f_{κ} (t)$ (Integer)
`fct_ID`_e	Function `f`_$ε$(`t`) identifier for energy. = 0 $ε = ε_{adjacent}$ = n $ε = ε_{0} \cdot f_{ε} (t)$ (Integer)
$C_{μ}$	Turbulent viscosity coefficient. Default = 0.09 (Real)
$σ_{κ}$	Diffusion coefficient for `k` parameter. Default = 1.00 (Real)
$σ_{ε}$	Diffusion coefficient for $ε$ parameter. Default = 1.30 (Real)
$P_{r} / P_{r t}$	Ratio between Laminar Prandtl number (Default 0.7) and turbulent Prandtl number (Default 0.9). (Real)

▸Example (Gas)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/B-K-EPS/5
GAS OUTLET (unit: kg_m_s)
#              RHO_I               RHO_0         
               .3828                   0
#     ITYP                           Psh       
         3                           0.0 		 
#                                      c                  lc
                                     605                 0.3
#blank line

#blank line
                    
#blank line

#             Rho0k0            Rho0Eps0     fct_k   fct_eps
                  20                   0         0         0
#                Cmu             Sigma-k       Sigma-epsilon              Pr/Prt
                   0                   0                   0                   0  
#blank line

/ALE/MAT/5
#     Modif. factor.
                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

Non-Reflecting Boundary formulation is based on Bayliss & Turkel. ^¹ The objective is to impose a mean pressure which fluctuate with rapid variations of pressure and velocity:
$\frac{\partial P}{\partial t} = ρ c (\frac{\partial}{\partial t} (V_{n}) - V_{n} \cdot div (V - V_{n} \cdot n)) + c \frac{(P_{\infty} - P)}{2 l_{c}}$
Pressure in the far field $P_{\infty}$ is imposed with a function of time. The transient pressure is derived from $P_{\infty}$ , the local velocity field V and the normal of the outlet facet:
- density, energy, temperature, turbulent energy and dissipation are imposed with a function of time as in Ityp = 2
- if the function number is 0, the neighbor element value is used to respect continuity
- acoustic impedance will be $ρ c$
- typical length $l_{c}$ is used to relax the effective pressure towards its imposed value. It should be large compared to the highest wave length of interest in the problem. The relaxation term acts as high pass filter whose frequency cut-off is:
  $f_{c} = \frac{c}{4 \cdot π \cdot l_{c}}$
Where, sound speed c and characteristic length $l_{c}$ are two required parameters (non zero).
The P_sh parameter enables shifting the output pressure which also becomes P-P_sh. If using $P_{s h} = P (t = 0)$ , the output pressure will be $Δ P$ , with an initial value of 0.0.
With thermal modeling, all thermal data ( $T_{0}, ρ_{0} C_{p}$ , ...) can be defined with /HEAT/MAT.
It is not possible to use this boundary material law with multi-material ALE /MAT/LAW37 (BIPHAS) and /MAT/LAW51 (MULTIMAT).

A. Bayliss, E. Turkel, "Outflow Boundary Condition for Fluid Dynamics", NASA-CR-170367, Institute for Computer Application in Science and Engineering, August 7, 1980