Ityp = 2

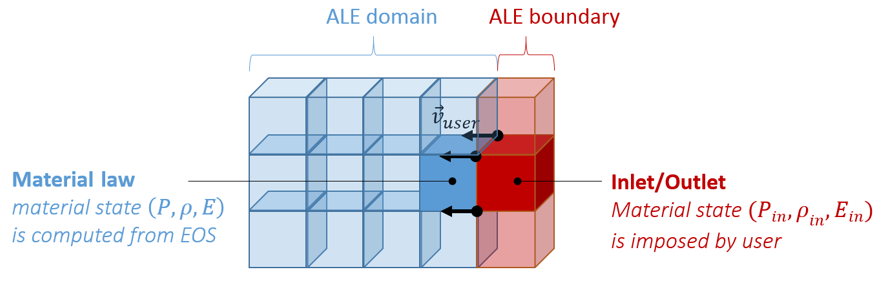
Block Format Keyword This law enables to model a material inlet/outlet by directly imposing its state. Input card is similar to /MAT/LAW11 (BOUND), but introduces two new lines to define turbulence parameters.

Format


(1)	(3)	(5)
/MAT/B-K-EPS/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$	$ρ_{0}$
`Ityp`	`P`_sh	`Fscale`_T

Ityp =2: General Inlet/Outlet


(1)	(2)	(3)	(5)	(6)	(7)
Blank Format
`fct_ID` $ρ$
`fct_ID`_p		`P`₀
`fct_ID`_E		`E`₀
$ρ_{0} κ_{0}$		$ρ_{0} ε_{0}$	`fct_ID`_k	`fct_ID`_e
$C_{μ}$		$σ_{κ}$	$σ_{ε}$		$P_{r} / P_{r t}$
`fct_ID`_T	`fct_ID`_Q

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. 3 (Real)	$[\frac{kg}{m^{3}}]$
$ρ_{0}$	Reference density used in E.O.S (equation of state). Default $ρ_{0}$ = $ρ_{i}$ (Real)	$[\frac{kg}{m^{3}}]$
`Ityp`	Boundary condition type. 1 = 0 Gas inlet (from stagnation point data) = 1 Liquid inlet (from stagnation point data) = 2 General inlet/outlet = 3 Non-reflecting boundary (Integer)
`P`_sh	Pressure shift. 3 (Real)	$[Pa]$
`Fscale`_T	Time scale factor. 3 (Real)
`fct_ID` $ρ$	Function $f_{ρ} (t)$ identifier for boundary density. 3 = 0 $ρ (t) = ρ_{i}$ > 0 $ρ (t) = ρ_{i} \cdot f_{ρ} (t)$ (Integer)
`fct_ID`_p	Function $f_{P} (t)$ identifier for boundary pressure.. 3 = 0 $P (t) = P_{0}$ > 0 $P (t) = P_{0} \cdot f_{P} (t)$ (Integer)
`P`₀	Initial pressure. 3 (Real)	$[Pa]$
`fct_ID`_E	Function $f_{E} (t)$ identifier for boundary energy. 3 = 0 $E (t) = E_{0}$ > 0 $E (t) = E_{0} \cdot f_{E} (t)$ (Integer)
`E`₀	Initial energy. 3 6 (Real)	$[Pa]$
$ρ_{0} κ_{0}$	Initial turbulent energy. (Real)	$[J]$
$ρ_{0} ε_{0}$	Initial turbulent dissipation. (Real)	$[J]$
`fct_ID`_k	Function $f_{κ} (t)$ identifier for turbulence modeling. = 0 $κ = κ_{a d j a c e n t}$ > 0 $κ = κ_{0} \cdot f_{κ} (t)$ (Integer)
`fct_ID`_$ε$	(Optional) Function $f_{ε} (t)$ identifier for turbulence modeling. = 0 $ε = ε_{a d j a c e n t}$ > 0 $ε = ε_{0} \cdot f_{ε} (t)$ (Integer)
$C_{μ}$	Turbulent viscosity coefficient. Default = 0.09 (Real)
$σ_{κ}$	Diffusion coefficient for $κ$ parameter. Default = 1.00 (Real)
$σ_{ε}$	Diffusion coefficient for $\dot{ε}$ parameter Default = 1.30 (Real)
$P_{r} / P_{r t}$	Ratio between Laminar Prandtl number (Default 0.7) and turbulent Prandtl number (Default 0.9). (Real)
`fct_ID`_T	Function $f_{T} (t)$ identifier for inlet temperature. = 0 `T = T`_adjacent = n $T = T_{0} \cdot f_{T} (t)$ (Integer)
`fct_ID`_Q	Function $f_{Q} (t)$ identifier for inlet heat flux. = 0 No imposed flux = n $Q = f_{Q} (t)$ (Integer)

▸Example (Gas)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/B-K-EPS/3
GAS INLET (unit: kg_m_s)
#              RHO_I
               .3828
#     ITYP                           Psh         Fscale_T
         2
#blank line
#  fct_RHO
         1
#    fct_P                           P_0
         0
#    fct_E                           E_0
         1                        253300
#             Rho0k0            Rho0Eps0     fct_k   fct_eps
                  20                   0         1         0
#                Cmu             Sigma-k       Sigma-epsilon              Pr/Prt
                   0                   0                   0                   0
# fct_T        fct_Q
/ALE/MAT/3
#     Modif. factor.
                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
CST
#                  X                   Y
                   0                   1
              1.0E20                   1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

Provided state is directly imposed to inlet boundary elements. This leads to the following inlet state:

$ρ_{i n} = ρ_{i} f_{ρ} (t)$

$P_{i n} = P_{0} f_{P} (t)$

$E_{i n} = {(ρ e)}_{i n} = E_{0} f_{E} (t)$

With this formulation, you may impose velocity on boundary nodes to be consistent with physical inlet velocity (/IMPVEL). /MAT/LAW11 - Ityp=0 and 1, are based on material state from stagnation point, where you do not need to imposed an inlet velocity.
The P_sh parameter enables shifting the output pressure which also becomes P-P_sh. If using $P_{s h} = P (t = 0)$ , the output pressure will be $Δ P$ , with an initial value of 0.0.
If no function is defined, then related quantity ( $P_{s t a g n a t i o n}, ρ_{s t a g n a t i o n}, T$ , or Q) remains constant and set to its initial value. However, all input quantities ( $P_{s t a g n a t i o n}, ρ_{s t a g n a t i o n}, T$ , and Q) can be defined as time dependent function using provided function identifiers. Abscissa functions can also be scaled using Fscale_T parameter which leads to use $f (F s c a l e_{t}, t)$ instead of $f (t)$ .
With thermal modeling, all thermal data ( $T_{0}, ρ_{0} C_{p}$ , …) can be defined with /HEAT.
It is not possible to use this boundary material law with multi-material ALE /MAT/LAW37 (BIPHAS)) and /MAT/LAW51 (MULTIMAT).
Specific volume energy E is defined as $E = \frac{E_{int}}{V}$ ,
Where

$E_{i n t}$

Internal energy. It can be output using /TH/BRIC.

Specific mass energy e is defined as $e = E_{i n t} / m$ . This leads to $ρ e = E$ . Specific mass energy e can be output using /ANIM/ELEM/ENER. This may be a relative energy depending on user modeling.