Ityp = 1

Block Format Keyword This law enables to model a liquid inlet condition by providing data from stagnation point. Liquid behavior is modeled with linear EOS. Input card is similar to /MAT/LAW11 (BOUND), but introduces two new lines to define turbulence parameters.

Format


(1)	(3)	(5)
/MAT/B-K-EPS/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}^{stagnation}$	$ρ_{0}^{stagnation}$
`Ityp`	`P`_sh	`Fscale`_T

Ityp =1: Liquid Inlet (from stagnation point data)


(1)	(2)	(3)	(5)	(6)	(7)
`node_ID`_v		`C`₁			`C`_d
`fct_ID`_$ρ$
`fct_ID`_p		$P_{0}^{stagnation}$
`fct_ID`_E		$E_{0}^{stagnation}$
$ρ_{0} κ_{0}$		$ρ_{0} ε_{0}$	`fct_ID`_k	`fct_ID`_$ε$
$C_{μ}$		$σ_{κ}$	$σ_{ε}$		$P_{r} / P_{r t}$
`fct_ID`_T	`fct_ID`_Q

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}^{stagnation}$	Initial stagnation density. 3 (Real)	$[\frac{kg}{m^{3}}]$
$ρ_{0}^{stagnation}$	Reference density used in E.O.S (equation of state). Default $ρ_{0}^{stagnation} = ρ_{i}^{stagnation}$ (Real)	$[\frac{kg}{m^{3}}]$
`Ityp`	Boundary condition type. 1 = 0 Gas inlet (from stagnation point data) = 1 Liquid inlet (from stagnation point data) = 2 General inlet/outlet = 3 Non-reflecting boundary (Integer)
`P`_sh	Pressure shift. 2 (Real)	$[Pa]$
`Fscale`_T	Time scale factor. 3 (Real)	$[s]$
`C`₁`node_ID`_v	Node identifier for velocity computation. 4 = 0 $v_{i n} = \min_{n o d e \in f a c e} (v_{n o d e} \cdot n)$ > 0 $v_{i n} = ‖ v_{n o d e_I D} ‖$ (Integer)
`C`₁	Liquid bulk modulus. 9 (Real)
`C`_d	Discharge coefficient. 5 Default = 0.0 (Real)
`fct_ID`_$ρ$	Function $f_{ρ} (t)$ identifier for stagnation density. 3 = 0 $ρ^{stagnation} (t) = ρ_{i}^{stagnation}$ > 0 $ρ^{s t a g n a t i o n} (t) = ρ_{i}^{s t a g n a t i o n} \cdot f_{ρ} (t)$ (Integer)
`fct_ID`_p	Function $f_{p} (t)$ identifier for stagnation pressure. 3 = 0 $P^{stagnation} (t) = P_{0}^{stagnation}$ > 0 $P^{s t a g n a t i o n} (t) = P_{0}^{s t a g n a t i o n} \cdot f_{P} (t)$ (Integer)
$P_{0}^{stagnation}$	Initial stagnation pressure. 3 (Real)	$[Pa]$
$E_{0}^{stagnation}$	Initial specific volume energy at stagnation point. 3 8 (Real)	$[Pa]$
$ρ_{0} κ_{0}$	Initial turbulent energy. (Real)	$[J]$
$ρ_{0} ε_{0}$	Initial turbulent dissipation. (Real)	$[J]$
`fct_ID`_k	Function $f_{κ} (t)$ identifier for turbulence modeling. = 0 $κ = κ_{adjacent}$ > 0 $κ = κ_{0} \cdot f_{κ} (t)$ (Integer)
`fct_ID`_$ε$	Function $f_{ε} (t)$ identifier for $ε$ . = 0 $ɛ = ɛ_{adjacent}$ > 0 $E^{s t a g n a t i o n} (t) = E_{0}^{s t a g n a t i o n} \cdot f_{E} (t)$ (Integer)
$C_{μ}$	Turbulent viscosity coefficient. Default = 0.09 (Real)
$σ_{κ}$	Diffusion coefficient for `k` parameter. Default = 1.00 (Real)
$σ_{ε}$	Diffusion coefficient for $ε$ parameter. Default = 1.30 (Real)
$P_{r} / P_{r t}$	Ratio between Laminar Prandtl number (Default 0.7) and turbulent Prandtl number (Default 0.9). (Real)
`fct_ID`_T	Function $f_{T} (t)$ identifier for inlet temperature. = 0 `T = T`_neighbor = n $T = T_{0} \cdot f_{T} (t)$ (Integer)
`fct_ID`_Q	Function $f_{Q} (t)$ identifier for inlet heat flux. = 0 No imposed flux = n $Q = f_{Q} (t)$ (Integer)

Comments

Provided gas state from stagnation point $(ρ_{stagnation}, P_{stagnation})$ is used to compute inlet gas state. Bernoulli is then applied.

$P_{stagnation} = P_{in} + \frac{ρ_{in} ν_{in}^{2}}{2}$

This leads to inlet state:
$ρ_{in} = \frac{C_{1} \cdot ρ_{stagnation}}{C_{1} + \frac{ρ_{stagnation} ν_{in}^{2}}{2} (1 + C_{d})}$
$P_{in} = P_{stagnation} - \frac{ρ_{stagnation} ν_{in}^{2}}{2} (1 + C_{d})$
${(ρ e)}_{in} = (1 - \frac{ρ_{in}}{ρ_{stagnation}}) P_{in} + E_{stagnation}$
The P_sh parameter enables shifting the output pressure, which also becomes P-P_sh. If using $P_{s h} = P (t = 0)$ , the output pressure will be $Δ P$ , with an initial value of 0.0.
If no function is defined, then related quantity $P_{s t a g n a t i o n}, ρ_{s t a g n a t i o n}, T$ and Q remains constant and set to its initial value. However, all input quantities $P_{s t a g n a t i o n}, ρ_{s t a g n a t i o n}, T$ and Q can be defined as time dependent function using provided function identifiers. Abscissa functions can also be scaled using Fscale_T parameter which leads to use $f (F s c a l e_{t}, t)$ instead of $f (t)$ .
Inlet velocity $ν_{in}$ is used in Bernoulli theory.
Discharge coefficient accounts for entry loss and depends on shape orifice.

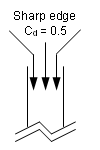
Figure 2.
With thermal modeling, all thermal data ( $T_{0}, ρ_{0} C_{p}$ , ...) can be defined with /HEAT/MAT.
It is not possible to use this boundary material law with multi-material ALE /MAT/LAW37 (BIPHAS)) and /MAT/LAW51 (MULTIMAT).
Definition of stagnation energy is optional. Default value is recommended: $E_{0}^{stagnation} = 0.0$ ; since linear EOS $Δ P = C_{1} μ$ does not depends on energy pressure is not affected and the initial energy is also set by you.
Specific volume energy E is defined as $= E_{i n t} / V$ ,
Where

$E_{i n t}$

Internal energy. It can be output using /TH/BRIC.

Specific mass energy e is defined as $e = E_{i n t} / m$ . This leads to $ρ e = E$ . Specific mass energy e can be output using /ANIM/ELEM/ENER. This may be a relative energy depending on user modeling.
Liquid bulk modulus is usually set to $C_{1} = ρ_{0} c_{0}^{2}$ .
Where,

$c_{0}$

Sound speed