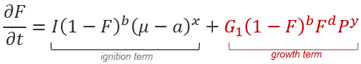/MAT/LAW41 (LEE_TARVER)

Block Format Keyword This material law describes detonation products using an ignition and growth model of a reactive material.

The Lee-Tarver model is based on the assumption that the ignition starts at local hot spots in the passage of shock front and grows outward from these sites. The reaction rate is controlled by the pressure and the surface area as in a deflagration process.

Format

(1)	(3)	(5)	(7)	(9)
/MAT/LAW41/`mat_ID`/`unit_ID` or /MAT/LEE_TARVER/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$	$ρ_{0}$
`Ireac`
$A^{r}$	$B^{r}$	$R_{1}^{r}$	$R_{2}^{r}$	$R_{3}^{r}$
$A^{p}$	$B^{p}$	$R_{1}^{p}$	$R_{2}^{p}$	$R_{3}^{p}$
$C_{ν}^{r}$	$C_{ν}^{p}$	$E_{Q}$
`itr`	$ε$	`F`_tol
`I`	`b`	`x`
`G`₁	`d`	`y`	`c`
`kappa`	`khi`	`tol`
`G`₂	`e`	`g`	`z`
`a`	`F`_igmax	`F`_G1max	`F`_G2min
`G`	`T`_i

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Interger, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
$ρ_{0}$	Reference density used in E.O.S (equation of state). Default = $ρ_{i}$ (Real)	$[\frac{kg}{m^{3}}]$
`Ireac`	Ignition and growth model flag. 1 = 1 (Default) Original 2-term-model (1980) ¹ = 2 Extended 3-term-model (1985) ² (Integer)
$A^{r}$	Reagents JWL parameter. (Real)	$[Pa]$
$B^{r}$	Reagents JWL parameter. (Real)	$[Pa]$
$R_{1}^{r}$	Reagents JWL parameter. (Real)
$R_{2}^{r}$	Reagents JWL parameter. (Real)
$R_{3}^{r}$	Reagents JWL parameter. 2 (Real)	$[\frac{J}{m^{3} \cdot K}]$ = $[\frac{Pa}{K}]$
$A^{p}$	Product JWL parameter. (Real)	$[Pa]$
$B^{p}$	Product JWL parameter. (Real)	$[Pa]$
$R_{1}^{p}$	Product JWL parameter. (Real)
$R_{2}^{p}$	Product JWL parameter. (Real)
$R_{3}^{p}$	Product JWL parameter. 2 (Real)	$[\frac{J}{m^{3} \cdot K}]$ = $[\frac{Pa}{K}]$
$C_{ν}^{r}$	Volumetric heat capacity for reagents. (Real)	$[\frac{J}{m^{3} \cdot K}]$ = $[\frac{Pa}{K}]$
$C_{ν}^{p}$	Volumetric heat capacity for product. (Real)	$[\frac{J}{m^{3} \cdot K}]$ = $[\frac{Pa}{K}]$
$E_{Q}$	Heat of reaction. (Real)	$[\frac{J}{m^{3}}]$
`itr`	Maximum number of iterations. 2 Default = 80 (Integer)
$ε$	Convergency tolerance. 2 Default = 10^-3 (Real)
`F`_tol	Burn fraction threshold. 3 Default = 10^-5 (Real)
`I`	Lee-Tarver parameter. (Real)	$[s^{- 1}]$
`b`	Lee-Tarver parameter. (Real)
`x`	Lee-Tarver parameter. (Real)
`G`₁	Lee-Tarver parameter. (Real)	$[s^{- 1} P a^{- Z_{g}}]$
`d`	Lee-Tarver parameter. (Real)
`y`	Lee-Tarver parameter. (Real)
`c`	Lee-Tarver parameter. (Real)
`kappa`	Numerical limiters. 6 Default = 99.0 (Real)
`khi`	Numerical limiters (extended model). 5 Default = 99.0 (Real)
`tol`	Numerical tolerance (extended model). 7 Default = 0.0 (Real)
`G`₂	Lee-Tarver parameter. (Real)	$[s^{- 1} P a^{- Z_{g 2}}]$
`e`	Lee-Tarver parameter. (Real)
`g`	Lee-Tarver parameter. (Real)
`z`	Lee-Tarver parameter. (Real)
`a`	Lee-Tarver parameter (extended model). (Real)
`F`_igmax	Ignition term limiter (extended model). 1 (Real)
`F`_G1max	Growth term #1 limiter (extended model). 1 (Real)
`F`_G2min	Ignition term #2 limiter (extended model). 1 (Real)
`G`	Shear modulus. 4 (Real)	$[Pa]$
`T`_i	Initial temperature. (Real)	$[K]$

Example (COMP-B)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW41/1
Military Comp-B (unit g,mm,µs,Mbar) ; Ref:UCRL-JC-111975,May 1993 (submittal 10th Det. Symposium)
#              RHO_0
               1.630
#    Ireac
         2
#                 Ar                  Br                 R1r                 R2r                 R3r
              1479.0            -0.05261                12.0                 1.2         2.268144E-5
#                 Ap                  Bp                 R1p                 R2p                 R3p
              5.5748              0.0783                 4.5                 1.2             0.34E-5
#                Cvr                 Cvp                  Eq
            2.487E-5                1E-5                .081
#     iter                           eps                Ftol
         0                             0                   0
#                  I                   b                   x
                44.0    0.22222222222222                   4
#                 G1                   d                   y                   c
               514.0    0.66666666666666                   2    0.22222222222222
#               kappa                 khi                 tol
                   0                   0                   0
#                 G2                   e                   g                   z
                 0.0                 0.0                 0.0                 0.0
#                  a              Figmax              FG1max              FG2min
                   0                 .30                 1.0                 1.0
#                  G                  Ti
              0.0354                 298
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

This material describes a mixture of reagents (unreacted explosive) and products (gas from detonation) for which the burn fraction is dictated by function $F (t)$ . There are two possible models to describe function $F$ depending on Ireac value:
- Ireac = 1: Original 2-term-model (1980) ¹(1)
- Ireac = 2: Extended 3-term-model (1985) ²(2)
  
  Where, $μ = ρ / ρ_{0} - 1$ , $a$ is a compression threshold under which ignition term has no contribution. Reaction rate is not computed if pressure is negative.
Both reagents and products are described with a JWL equation of state. The temperature dependency form is used $P (ν, T) = A e^{- R_{1} ν} + B e^{- R_{2} ν} + R_{3} T / ν$ where, $R_{3} = ω c_{ν}$ .
Consequently, a set of JWL parameters must be defined for both reagents and products:
- Reagents:(3)
  $P_{r} (ν, T) = A_{r} e^{- R_{_{1}}^{r} ν} + B_{r} e^{- R_{_{2}}^{r} ν} + R_{_{3}}^{r} T / ν$
- Products:(4)
  $P_{p} (ν, T) = A_{p} e^{- R_{_{1}}^{p} ν} + B_{p} e^{- R_{_{2}}^{p} ν} + R_{_{3}}^{p} T / ν$
For reagents, $B_{r}$ is negative so that the solid undergoes tension and $ω_{r}$ is set to the initial Gruneisen coefficient.

An iterative solver is used to ensure equilibrium between reagents and products: $P_{r} = P_{p}$ .

itr is the maximum number of iteration and eps is the convergency tolerance $(|P_{r} - P_{p}| < e p s)$ .
$F_{t o l}$ is such as:
- $F < F_{t o l}$ : reaction has not started
- $F > 1 - F_{t o l}$ : reaction has finished
Shear modulus is used for sound speed calculation: (5)
$c^{2} = \frac{1}{ρ_{0}} (\frac{d P}{d μ} + \frac{4}{3} G)$
$k h i$ is a numerical limiter such as: (6)
$F (t_{n + 1}) - F (t_{n}) \leq k h i$
$k a p p a$ is a numerical limiter such as reaction is not calculated if $Q \geq k a p p a \cdot P$ .
Where, $Q$ = Pseudo viscosity (from shock front).
$t o l$ is a tolerance parameter.
$d F / d t$ is updated using $F + F_{t o l}$ instead of $F$ in the right hand term of the 3-term-model.
This material is not yet compatible with ALE.

¹ Lee E.L. and Tarver C.M., "Phenomenological model of shock initiation in heterogeneous explosives" Phy. Fluids Vol. 23, No. 12, December 1980.

² Tarver C.M., Hallquist J.O. and Erickson L.M., "Modeling Short Pulse Duration Shock Initiation of Solid Explosives", 8^th International Symposium on Detonation, Albuquerque, NM, July 1985, pp 951-961