Brake Squeal Analysis
Analysis of the noise, vibration and harshness of brake systems is an essential study from the standpoint of the automotive industry. An important aspect of vehicle comfort is the quietness of the brake system.
Often low velocity braking maneuvers are accompanied by heavy noise occurrences. Although these do not affect the braking performance or safety, they result in noise pollution and customer insecurity. The consequence of this is an investment of time and money on developing silent brake systems. Brake noise solutions drive the development of quiet brake systems, warranty cost and sometimes even vehicle mass.
- Judder: ~10 Hz at very low vehicular speeds
- Groan: ~100 Hz at low vehicular speeds
- Moan: ~100 Hz at moderate vehicular speeds
- Squeal: >1 kHz at higher vehicular speeds
In brake assemblies, these dynamic instabilities are kinetic friction induced. Judder is more of a vibration and harshness issue - a pulsation between brake and pads transmitted to the steering primarily because of non-uniform friction between brake and pads. This can be caused, for example, due to some manufacturing defects. The other instabilities are caused either because of mode coalescence, that is, the coupling of neighboring modes (squeal) or stick-slip motion resulting from a negative friction velocity gradient (groan/moan).
There are two ways of studying these instabilities: transient and modal analysis. While the former is required for correlation with test data, the latter is preferred due the computationally-expensive nature of the former. The modal analysis will give the engineer an idea of whether these instabilities exist in the brake assembly, and hence the mechanics that needs to be accurately modeled is the friction between brake and pads.

On the other hand, the prediction of groan/moan, must account for the negative friction-velocity gradient indicated in Figure 1. A braking maneuver typically occurs at a particular vehicle speed (or, equivalently, rotor angular velocity). Another modeling issue that needs to highlighted is that in OptiStruct, the contact algorithms regulate friction with respect to the slip distance rather than slip velocity as shown in Figure 1. Therefore, while using the current capabilities, it is not possible to predict the low frequency phenomenon of groan/moan, one can predict the high frequency phenomenon of squeal, by prescribing rotor rotation rather than rotor spin. Thus, currently, the rotational speed of the disc is not relevant in the OptiStruct brake squeal solution sequence.
SPCD is used to prescribe rotor rotation for brake squeal, instead of prescribing a steady spin of the rotor. As long as gyroscopic effects are ignored and kinetic friction is a constant value (independent of velocity), prescribing rotation using SPCD is equivalent to prescribing rotational speed. The important outcome is that the contact nodes are in kinetic friction mode - it does not matter how fast or how far you move this using SPCD. This is the case for modeling squeal, which happens due to mode coupling via friction and at relatively high speeds (as opposed to groan), where the coefficient of friction is independent of velocity.
Finally, since the brake system has components (more precisely, the rotor) that rotate, this necessitates modeling rotor dynamics. However, since instabilities are associated with low velocity braking maneuvers and are caused by dynamic friction, ignoring rotor dynamics is a reasonable approximation and can be considered a safe modeling technique for the modal approach that is primarily associated with prediction of the existence of instabilities. Once the instability has been identified using the modal method and when the transient approach is used to predict test data, the model must then, of course, include rotor dynamic effects to capture the physics of the phenomenon accurately.
- A nonlinear static solution to obtain the static equilibrium of brake assembly under the applied loads. The contact between the disc and the pads are modeled using N2S or S2S contacts. In this subcase, pressure loads clamp the pads to the disc. Then an SPCD load is applied which rotates the disc relative to the pads by certain angular units. This number should be chosen such that the converged gap contacts are in slip friction, yet making sure that the problem is still in the small displacement domain.
- This is followed by the extraction of the complex eigenvalues via Complex Eigenvalue Analysis. The initial Nonlinear Static solution subcase is referenced here using STATSUB(BRAKE).
It must be ensured during the nonlinear static solution, by prescribing rotation, that the contact between the disc and the pads is in the dynamic friction status when the solution converges. The complex eigenvalue solution is carried out by projecting the system matrices into a subspace determined by the modes of a symmetric version of the final stiffness matrix. The unstable modes arise primarily since the stiffness matrix is not symmetric due to dynamic (slip) friction effects.
Prior to this development, the OptiStruct capabilities of analyzing brake systems required the importing of the asymmetric friction matrix using K2PP (or some such equivalent) from an external source into the complex eigensolver. The development of the brake squeal solution sequence in OptiStruct will eliminate this step and provide the solution in a single seamless run (for more information on the previous method, see the Usage section of Complex Eigenvalue Analysis).
Implementation
From the first nonlinear subcase, three important results are sourced - the geometric stiffness matrix ( ), and two converged gap stiffness matrices - the complete gap matrices ( ), and gap matrices with normal stiffness terms only ( ). The former is asymmetric since it includes the tangential friction terms, while the latter is a symmetric version which will be used to span the modal subspace. accounts for geometric stiffness from the brake pressure loads.
The modal complex eigensolution subcase references the initial nonlinear subcase as a brake load (using the STATSUB(BRAKE) entry). Let the original mass, damping and stiffness matrices of the system be , , and , respectively.
The first step in this subcase is to find the modes ( ) and eigenvalues ( ) of the system with its original mass matrix, but the following stiffness:
The stiffness matrix which contains information about the total state of the system is:
The modal projections of the system matrices is given by:
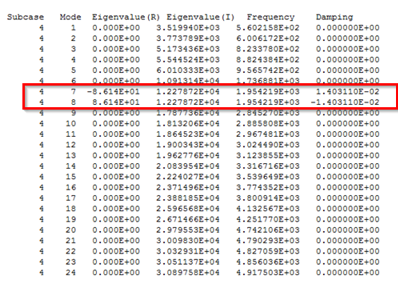
An eigenvalue analysis on this system will yield information on the system stability. The eigenvalues are of the form , from which the damped frequency and equivalent damping can be obtained. An eigenvalue with a positive real part or negative damping indicates instability.
Input/Output
Input
- An initial Nonlinear Static Analysis subcase which represents the Brake loads (Pressure) including a prescribed rotation (SPCD).
- A subsequent Complex Eigenvalue Analysis subcase which references the initial Nonlinear Static Analysis subcase via STATSUB(BRAKE).
SUBCASE 1
LABEL nonlinear_static_brake_loads
ANALYSIS NLSTAT
SPC = 1
LOAD = 4
NLPARM = 1
SUBCASE 2
LABEL complex_eigenvalue
ANALYSIS MCEIG
SPC = 1
METHOD(STRUCTURE) = 2
CMETHOD = 3
STATSUB(BRAKE) = 1
Output