Milieu isotrope / anisotrope (matériaux doux)

Introduction

Le milieu étudié peut être isotrope ou anisotrope . Autrement dit, la loi de comportement est :

• indépendante de la direction du champ appliqué (milieu isotrope)
• dépendante de la direction du champ appliqué (milieu anisotrope)

Ces deux cas sont présentés dans les blocs ci-après.

Milieu isotrope

Les milieux isotropes sont caractérisés par une loi de comportement indépendante de la direction du champ appliqué.

Les champs et sont toujours colinéaires.

La relation entre et est une relation scalaire qui s'écrit: B= μ .H

Remarque :

• si approximation linéaire :

  μ constant ⇒ on peut écrire B= μ .H

• si approximation non linéaire :

  μ variable ⇒ il vaut mieux écrire B= μ (H).H

Milieu anisotrope

Les milieux anisotropes sont caractérisés par une loi de comportement dépendante de la direction du champ appliqué.

Les champs et ne sont pas colinéaires.

La relation entre et est une relation vectorielle qui s'écrit :

avec μ tenseur de perméabilité :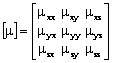

Remarque :

• si approximation linéaire :

  μ_ij constant ⇒ on peut écrire

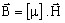
• approximation non linéaire :

  μ_ij variable ⇒ il vaut mieux écrire

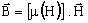
Remarque au sujet de l'anisotropie …

L'anisotropie peut être :

• une anisotropie cristalline liée à la structure cristalline du matériau
• une anisotropes liée au feuilletage (paquets de tôles), dans ce cas, on parle alors de « pseudo-anisotropie ». Cette forme d'anisotropie est prise en compte par un type spécifique de région appelée « Région magnétique feuilletée non conductrice » (voir le chapitre Physique : Principes )

Anisotropie cristalline (dans le plan de la tôle)

Les modèles qui permettent de prendre en compte l'anisotropie cristalline, sont des modèles qui se focalisent sur l'anisotropie 2D (ie. uniquement dans le plan de la tôle ).

Ces modèles respectent principalement les caractéristiques magnétiques mesurées des tôles dans leurs directions principales (direction de laminage : DL, et direction transverse : DT).

On peut citer (extrait de la thèse de Nahil Hihat):

• le modèle de séparation des axes NIYS75
• le modèle des deux axes HLN84
• le modèle elliptique et le modèle elliptique avec rotation des axes DNP83
• des modèles d'anistropies empiriques …

Directions préférentielles d'une tôle :

• DL : directions de laminage
• DT : direction transverse
• DN : direction normale

Bibliographie

Des informations complémentaires sur la modélisation des matériaux magnétiques anisotropes sont disponibles dans les documents suivants :

• « Modèles Quasi 3D pour l'Analyse de Structures présentant une Anisotropie 3D »thèse de Nabil HIHAT – 2010Université Lille Nord de FranceUArtois
• « Lois d'aimantation anisotropes et non linéaires : modélisation et validation expérimentale »thèse de Thierry PERA – 1994INPG
• « Contribution à la modélisation bidimensionnelle et tridimensionnelle des phénomènes d'anisotropie dans les transformateurs triphasés » thèse de Jean Marc DEDULLE – 1990 – INPG

Références relatives aux modèles semi-analytique 2D (plan de la tôle) :

• NIYS75 T. Nakata, Y. Ishihara, K. Yamada et A. Sasano :

  Non-linear analysis of rotating flux in the t-joint of a three-phase, three-limbed transformer core.

  In proceedings of Soft Magnetic Materials 2 Conference, pages 57-62. 1975.

• HLN84 D. Huttenloher, H.W. Lorenzen et D. Nusheler :

  Investigation of the importance of the anisotropy of cold rolled electrical steel sheet. IEEE Transactions on Magnetics , 20(5):1968 -1970, 1984.

• DNP83 A. Di Napoli et R. Paggi :

  A model of anisotropic grain-oriented steel.

  IEEE Transactions on Magnetics , 19(4):1557-1561, 1983.

Difficultés de modélisation des milieux anisotropes

Pour un milieu anisotrope, la perméabilité se présente sous une forme tensorielle, dont chacune des composantes dépend du champ appliqué.

La relation vectorielle B(H) s'écrit alors sous la forme de 3 familles de courbes :

• Bx (Hx, Hy, Hz)
• By (Hx, Hy, Hz)
• Bz (Hx, Hy, Hz)

La description de ce type de courbes au niveau expérimental est très délicate puisqu'il faut être capable de mesurer à la fois le module et la direction de l'induction magnétique en fonction du champ H. On se limite, en général, à des mesures dans les directions où le champ magnétique et l'induction sont parallèles.

En supposant que ces caractéristiques soient fournies, il faut ensuite pouvoir les introduire au niveau du logiciel et que ce dernier soit capable de réaliser les interpolations nécessaires lors du traitement numérique.

Pour ces différentes raisons, on peut dire qu'à l'heure actuelle :

• il existe des modèles simplifiés mais dont les domaines de validité sont limités
• les modèles anisotropes non linéaires sont encore du domaine de la recherche

Modèles simplifiés

Les modèles simplifiés se basent en général sur une séparation des phénomènes suivant les axes principaux du matériau.

La méthodologie consiste à exprimer la relation vectorielle B(H) à partir des trois directions principales du matériau et de réaliser l'interpolation la plus représentative possible (interpolation linéaire, elliptique, …).

Chaque classe de matériau doit être examinée différemment (matériaux doux, aimants permanents).

… dans Flux: modèle linéaire

Le modèle simplifié proposé dans Flux pour le modèle linéaire est un modèle de séparation des axes avec interpolation linéaire .

La relation vectorielle entre et qui s'écrit : peut alors se mettre sous la forme de 3 courbes : B x (H x ), B y (H y ), B z (H z ).

Le tenseur de perméabilité s'écrit :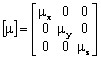

Ce formalisme purement mathématique est très simple et très commode au niveau de la résolution. Il traduit le fait qu'au niveau macroscopique l'induction et le champ sont parallèles dans les directions principales : direction privilégiée, direction transversale et troisième axe.

Pour une tôle il pourra s'agir de la direction de laminage, de la direction transverse et de la direction orthogonale.

Pour un aimant permanent, il s'agira de la direction d'aimantation, et des directions perpendiculaires à cet axe.

Bibliographie

Des informations complémentaires sur la modélisation des matériaux magnétiques anisotropes sont disponibles dans les documents suivants :

• « Lois d'aimantation anisotropes et non linéaires : modélisation et validation expérimentale »thèse de Thierry PERA – 1994INPG
• « Contribution à la modélisation bidimensionnelle et tridimensionnelle des phénomènes d'anisotropie dans les transformateurs triphasés » thèse de Jean Marc DEDULLE – 1990INPG

… dans Flux : modèle non linéaire

Le modèle utilisé dans Flux pour prendre en compte les matériaux linéaires anisotropes n'est pas généralisable au cas non linéaire.

Un nouveau modèle avec interpolation elliptique a donc été introduit pour les matériaux non linéaires (en 2D). Il n'est pas détaillé dans ce document, mais les références bibliographiques sont données dans le bloc ci-dessous.

Biroet al., 2010 Biro, O., Außerhoger, S., Preis, K., and Chen, Y. (2010). A modified elliptic model of anisotropy in nonlinear magnetic materials. COMPEL : The Internationnal Journal for Computation and Mathematics in Electrical and Electronic Engineering , 29(6):1482 – 1492.

Dedulle et al., 1990 Dedulle, J.-M., Meunier, G., Foggia, A., Sabonnadiere, J.-C., and Shen, D. (1990). Magnetic fields in nonlinear anisotropic grain-oriented iron-sheet. IEEE Transactions on Magnetics , 36(2):524 – 527.

Napoli and Paggi, 1983 Napoli, A. D. and Paggi, R. (1983). A model of anisotropic grain-oriented steel. IEEE Transactions on Magnetics , 19(4):1557 – 1561.