Limites du domaine d'étude, généralités
Phénomènes électromagnétiques
Dans l'étude de phénomènes électromagnétiques il est nécessaire de modéliser le dispositif et l'air qui l'entoure. En effet les grandeurs étudiées en électromagnétisme (champs électriques, champs magnétiques), ne sont pas nulles dans l'air ou dans le vide, contrairement à d'autres domaines de la physique (mécanique par exemple) ou l'air n'est pas pris en compte.
Méthode des éléments finis
La méthode des éléments finis est basée sur la subdivision du domaine d'étude complet en un nombre fini de sous domaine de dimension finie.
Le problème physique est posé sous la forme d'une équation différentielle ou aux dérivées partielles à satisfaire en tout point d'un domaine, avec des conditions aux limites sur les bords nécessaires et suffisantes pour que la solution soit unique.
Pour résoudre un problème par la méthode des éléments finis, il faut donc :
- donner des limites à la zone modélisée, c'est-à-dire définir les limites ou frontières du domaine,
- donner des conditions aux limites sur les bords, c'est-à-dire définir les valeurs de la variable d'état (potentiel, température) sur les frontières du domaine.
Contradiction apparente
La méthode des éléments finis impose de donner des limites à l'espace de travail alors que les phénomènes électromagnétiques sont « illimités ».
En d'autres termes :
Les domaines ouverts ne sont pas modélisables avec la méthode des éléments finis car il est impossible de subdiviser un domaine infini en un nombre fini de sous domaines finis.
Limites du domaine d'étude : les différentes méthodes
Pour pallier cette contradiction, différentes méthodes peuvent être utilisées.
Une première méthode (méthode de troncature) consiste à fermer le domaine d'étude par une frontière suffisamment éloignée de façon à ne pas perturber les résultats.
Une seconde méthode consiste à utiliser une transformation ramenant le domaine ouvert à un domaine fermé.
Ces deux méthodes sont décrites dans les paragraphes suivants.
Limites du domaine d'étude : méthode de troncature
La méthode de troncature consiste à fermer le domaine d'étude par une frontière suffisamment éloignée de façon à ne pas perturber les résultats.
Le dispositif est placé dans une boîte d'air, et l'infini est assimilé à une frontière fermée et lointaine. La taille de la boîte est ajustée pour que l'on puisse négliger les effets de cette approximation.
L'utilisateur doit déterminer la « quantité d'air » à modéliser à l'extérieur du dispositif ; c'est-à-dire évaluer la distance à partir de laquelle il estime que les champs étudiés sont nuls ou suffisamment faibles pour pouvoir être négligés.
Méthode de troncature : inconvénients
La méthode de troncature présente un certain nombre d'inconvénients :
- coût relativement élevé en terme de nombre d'inconnues
- valeurs de champ peu significatives au voisinage de la frontière
Modélisation de l'infini : utilisation de transformation
Pour remédier à ces inconvénients, une seconde méthode consiste à utiliser une transformation ramenant le domaine ouvert à un domaine fermé .
L'idée de base est de se dire : puisque nous ne pouvons pas mailler le domaine ouvert, transformons ce domaine ouvert en domaine fermé.
Utilisation d'une transformation, principe
L'espace initial est décomposé en deux domaines :
- un domaine intérieur fermé Eint
- un domaine extérieur ouvert Eext
Cet espace initial à frontières ouvertes est transformé en un espace final à frontières fermées de la façon suivante :
- le domaine intérieur (Eint) n'est pas modifié.
- le domaine extérieur (Eext) est relié à un domaine fermé (Eext_image) par le biais d'une transformation spatiale T.
L'espace final est donc composé de deux domaines :
- un domaine intérieur fermé Eint
- un domaine extérieur fermé Eext_image
Ces deux domaines (fermés) sont maillés avec des éléments finis classiques.
Illustration : Representation du domaine extérieur
Utilisation d'une transformation, principe (suite)
Pour tenir compte de la transformation dans les équations, on considère que :
- les formulations éléments finis ne sont pas modifiés (la variable d'état du domaine initial et la variable d'état du domaine image sont égales)
- de nouveaux types d'éléments finis (les éléments finis transformés) sont capable de modéliser l'infini.
Illustration : Représentation du domaine extérieur
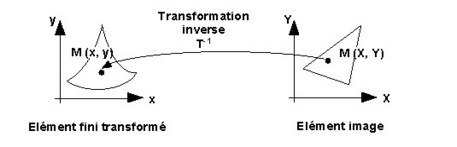
Choix de la transformation
On peut théoriquement utiliser beaucoup de transformations spatiales. La transformation de l'espace réel à l'espace image doit être bijective. Elle doit également avoir des propriétés de continuité et de dérivabilité sur et entre les éléments…
En pratique, les transformations utilisées dans le logiciel tiennent comptent de différents critères d'efficacité : qualité de la solution obtenue pour un nombre d'éléments ou d'inconnues, facilité d'implantation…