Pertes fer à posteriori : modèle de Bertotti

Le modèle de Bertotti modifié

Le modèle de Bertotti mis en œuvre dans Flux est une version modifiée du modèle standard bien connu de Bertotti pour les pertes fer. Ces modèles appartiennent à la grande famille des méthodes de type Steinmetz qui établissent des relations empiriques entre les pertes spécifiques (en W/kg) dans une tôle d'acier électrique et la fréquence de l’induction magnétique dans le matériau.

Puisque les phénomènes d'hystérésis, qui sont la cause des pertes fer, demandent une représentation dans le domaine temporel, le modèle standard de Bertotti est reformulé dans Flux pour l'appliquer à des formes d'ondes non-sinusoïdales, pour donner aux utilisateurs plus de degrés de liberté, pour prendre en compte les éventuelles composantes continues non-nulles de B et pour unifier les équations et les paramètres à utiliser aussi bien en transitoire qu'en fréquentiel. En raison de ces spécificités, l'implémentation du modèle de Bertotti dans Flux est dite "modifiée" : en d'autres termes, il a été adapté ou optimisé pour fonctionner de manière robuste dans le contexte des calculs Éléments Finis.

Selon le modèle de Bertotti modifié, la densité de pertes fer (directement liée aux pertes spécifiques par la masse volumique) dans un empilement de tôles d'acier électrique peut être décomposée en une somme de trois termes : à savoir, les termes de pertes hystérétiques, classiques (appelées aussi par courants de Foucault) et par excès. Dans chaque point du matériau décrit par une région magnétique feuilletée non conductrice, dans le domaine fréquentiel l'équation suivante s'applique :

où

représente la densité moyenne des pertes fer, en W/m³ ;
$λ_{F}$ est le coefficient de foisonnement de l'empilement de tôles ;
$k_{1}$ est le coefficient des pertes hystérétiques ;
$α_{1}$ est l'exposant des pertes hystérétiques ;
$k_{2}$ est le coefficient des pertes classiques ;
$α_{2}$ est l'exposant des pertes classiques ;
$k_{3}$ est le coefficient des pertes par excès ;
$α_{3}$ est l'exposant des pertes par excès ;
$f_{}$ est la fréquence de l’induction magnétique, qui est supposée varier périodiquement dans le temps ;
$B_{max}$ (en teslas) est l'amplitude maximale que l'induction magnétique homogénéisée peut atteindre au cours d'une période ${T=1/f}_{}$ au point de la région feuilletée considéré ; cette valeur est automatiquement calculée par Flux à travers l'induction magnétique et le coefficient de foisonnement $λ_{F}$ .

De manière similaire, dans le domaine temporel l'équation suivante s'applique :

où

représente la densité de pertes fer instantanée, en W/m³ ;
T est la période de l'induction magnétique ;
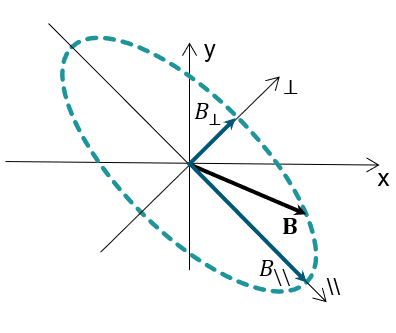
et sont les excursions maximales par rapport à leur composante continue, sur la période T respectivement des projections longitudinale et transversale de l'induction magnétique homogénéisée ; en chaque point de la région feuilletée, la direction longitudinale est définie comme la direction de B au pas de temps où l'induction magnétique atteint sa valeur maximale pendant la période considérée, alors que la direction transversale est orthogonale à la longitudinale, comme montré dans l'image ci-dessous ;
est le module de la dérivée temporelle de l'induction magnétique homogénéisée, qui a été au préalable décomposée dans ses projections longitudinale et transversale définies ci-dessus ;
les coefficients $k_{i}$ et les exposants $α_{i}$ sont les mêmes de l'équation dans le domaine fréquentiel ci-dessus.

Dans les équations ci-dessus, le premier terme dénommé comme hystérétique et caractérisé par les paramètres $k_{1}$ et $α_{1}$ , représente les phénomènes d'hystérésis statique et permet d'évaluer ce qui est appelé densité de pertes hystérétiques (voir cette page pour plus d'informations). Le deuxième et troisième termes dénommés comme classiques (ou par courant de Foucault) et par excès, respectivement, prennent en compte aussi les phénomènes d'hystérésis dynamique, de manière que toute l'équation de Bertotti modifié permet d'évaluer la totalité de la densité de pertes fer.

Les coefficients $k_{i}$ et les exposants $α_{1}$ ci-dessus sont spécifiques à une nuance d'acier électrique donnée ou à un type de tôle. Ils sont généralement déterminés par une procédure de fittage sur les valeurs de mesures magnétiques fournies par les fabricants dans les fiches techniques (c.-à-d., un tableau de pertes spécifiques mesurées en fonction de l'induction magnétique $B_{max}$ à plusieurs fréquences). Pour aider les utilisateurs à déterminer les paramètres du modèle de Bertotti, Flux fournit un outil de Caractérisation de matériaux, basé sur le langage Compose.

A partir de la densité de pertes fer en tous les points et des fonctions de forme des Éléments Finis, Flux intègre efficacement cette quantité dans le volume des régions magnétiques feuilletées non conductrices pour calculer les pertes fer à posteriori.

Utilisation du modèle de Bertotti modifié dans Flux

Le modèle de Bertotti modifié n'étant utilisé que lors des opérations de post-traitement, il s'agit d'une définition complémentaire à ajouter à la caractéristique B(H) du matériau doux de la région. Les paramètres de Bertotti peuvent être renseignés :

soit dans la boîte de dialogue du Matériau, dans l'onglet Pertes fer dédié, où l'utilisateur doit cocher la case Modèle pour le calcul des pertes fer et ensuite définir les valeurs pour les Coefficients et pour les Exposants dans les sous-onglets correspondants ;
soit pendant les phases de post-traitement à travers la boîte de dialogue fournie pour le calcul de pertes fer sur régions ou pour le multi-paramètrique.

Dans Flux, le modèle de Bertotti modifié est disponible en 2D, Skew et 3D pour toutes les applications Magnétiques, c.-à-d. Transitoire, Harmonique et Statique (en Mode Avancé uniquement pour cette dernière) et peut uniquement être appliqué aux Régions magnétiques feuilletées non conductrices.