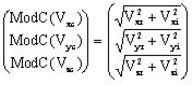Fonctions modules : ModV, ModC et Mod

Avant de commencer

Les fonctions modules (module vectoriel, module complexe et module général) permettent le calcul du module de grandeurs scalaires et vectorielles, réelles ou complexes.

Avant la description des fonctions module, un rappel des notations est présenté dans les blocs suivants.

Grandeurs scalaires : notations

Pour définir les fonctions modules sur les grandeurs scalaires (réelles et complexes), nous utiliserons les notations suivantes :

• pour un scalaire réel : A

• pour un scalaire complexe : I

  tel que I = Ir + j Ii

  où Ir et Ii sont des scalaires réels

Grandeurs vectorielles : notations

Pour définir les fonctions modules sur les grandeurs vectorielles (réelles et complexes), nous utiliserons les notations suivantes :

• pour un vecteur réel : V

  tel que

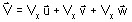
  où Vx , Vy , et Vz , sont des scalaires réels

• pour un vecteur complexe : Vc

  tel que

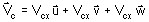
  où Vcx , Vcy , et Vcz sont des scalaires complexes

  Il est également possible d'écrire le vecteur complexe sous la forme :

  $\overrightarrow{Vc}=\overrightarrow{Vr}+j \overrightarrow{Vi}=\left(\begin{array}{c}Vxr\\ Vyr\\ Vzr\end{array}\right)+j\left(\begin{array}{c}Vxi\\ Vyi\\ Vzi\end{array}\right)=\left(\begin{array}{c}Vxr+jVxi\\ Vyr+jVyi\\ Vzr+jVzi\end{array}\right)=\left(\begin{array}{c}Vcx\\ Vcy\\ Vcz\end{array}\right)$

  où Vxr , Vyr , Vzr , Vxi , Vyi et Vzi sont des scalaires réels.

Module vectoriel : fonction ModV

La fonction ModV (X) retourne le module vectoriel d'un vecteur X

(vecteur réel ou vecteur complexe).

• Si V est un vecteur réel, ModV(V) est un scalaire réel tel que :

  $ModV\left(V\right)=\sqrt{Vx²+Vy²+Vz²}$

• Si V c est un vecteur complexe, ModV(V c ) est un scalaire complexe tel que :

  $ModV\left(Vc\right)=ModV\left(Vr\right)+j ModV\left(Vi\right)= \sqrt{Vxr²+Vyr²+Vzr²}+j \sqrt{Vxi²+Vyi²+Vzi²}$

Module complexe : fonction ModC

La fonction ModC (X) retourne le module complexe d'un complexe X

(scalaire complexe ou vecteur complexe).

• Si I est un scalaire complexe, ModC(I) est un scalaire réel tel que :

  

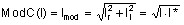
• Si V c est un vecteur complexe, ModC(Vc ) est un vecteur réel tel que :

  $ModC\left(Vc\right)=\left(\begin{array}{c}ModC\left(Vcx\right)\\ ModC\left(Vcy\right)\\ ModC\left(Vcz\right)\end{array}\right)=\left(\begin{array}{c}\sqrt{Vxr²+Vxi²}\\ \sqrt{Vyr²+Vyi²}\\ \sqrt{Vzr²+Vzi²}\end{array}\right)$

Module général : fonction Mod

La fonction Mod (X) retourne le module général de X. Quel que soit le type d'argument X (scalaire ou vecteur, réel ou complexe) de la fonction Mod, le résultat Mod(x) est un scalaire réel.

• Si I est un scalaire complexe, Mod(I) est un scalaire réel tel que :

  

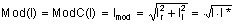
• Si V c est un vecteur complexe, Mod(V c ) est un scalaire réel tel que :

  

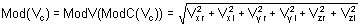
Résumé

Les résultats des fonctions modules (ModV, ModC et Mod) sont rassemblés dans les tableaux ci-dessous.