Blunt Body

Correlation to calculate HTC in forced convection in case of crossflow conditions over a body. This correlation supports several shapes of the body in crossflow.

Type: Body in Crossflow Nu
Subtype: Body in Crossflow

Table 1. Inputs List
Index	UI Name (.flo label)	Description
1	Shape (SHAPE_ID)	Shape of the body in the cross flow. The shapes available in the correlation are mentioned in the Formulation section.
2	Velocity Input Type (VEL_ID)	Methods available for the user for velocity input: Chamber User Input RPM based Further discussions are in the Formulation section.
3	Velocity (FLOW_VEL)	This is activated only if User Input is selected as the “Velocity Input Type”. It takes the user input velocity.
4	Characteristic Length (CHAR_LEN)	The characteristic length/diameter of the fluid flow. “d” in the Formulation section.
5	Outer Radius (OUTER_R)	The stator outer radius. This is activated only if RPM Based is selected as the “Velocity Input Type”. If “Auto”, then Outer Radius = 0.5 * Characteristic Length.
6	Tip Speed Ratio (TIP_SPD_RATIO)	The frame tip speed ratio, user-defined.
7	HTC Multiplier (HTC_MULT)	A constant multiplier to scale the value of heat transfer coefficient obtained from the correlation.

Formulation

This correlation uses a Nusselt number that can be found in references 1, 2, and 3. A linear interpolation is used if the Re is in the transitional regime.

Reynolds Number:

R e = \frac{ρ V_{e x t} d}{μ_{T_{}}}

With:

$V_{e x t}$ : The external fluid velocity.

$d$ : The characteristic length/diameter of the fluid flow.

$μ_{T}$ : The external fluid flow viscosity, at the film temperature.

$ρ$ : The external fluid density.


Velocity Input Type	Comments	Formulation
Chamber	This is the default method. This takes the velocity that is calculated in the fluid chamber attached to the convector.
User Input	In this method, you can directly input the velocity.
RPM Based	This method requires the outer radius and tip speed ratio for calculation of the velocity. It is further explored in Formulation section.	$V_{e x t} = \frac{ω * O R}{T i p S p e e d R a t i o}$ With: $ω$ : The angular speed of the rotor. $O R$ : The outer radius. $T i p S p e e d R a t i o$ : The user-defined tip speed ratio.

Nusselt’s number:

N u = C R e^{m} P r^{0.35}


Shape Name in GUI	Re	C	m
Square	2.510³– 810³	0.180	0.699
Square	5*10³ - 10⁵	0.102	0.675
Rhombus	5*10³ - 10⁵	0.25	0.588
Horizontal Ellipse	2.510³– 1.510⁴	0.25	0.612
Vertical Ellipse	310³– 1.510⁴	0.096	0.804
Horizontal Hexagon	5*10³ - 10⁵	0.156	0.638
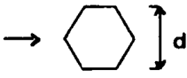
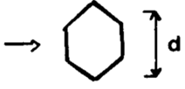
Vertical Hexagon	510³– 1.9510⁴	0.162	0.638
Vertical Hexagon	1.95*10⁴ - 10⁵	0.0395	0.782
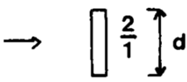
Thick Vertical Plate	310³– 210⁴	0.264	0.66
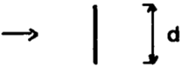
Thin Vertical Plate	410³– 1.510⁴	0.232	0.731
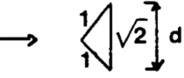
Horizontal Triangle	310³– 210⁴	0.246	0.61
Cylinder	This follows Churchill-Bernstein convection correlation. For more information, see Heat Transfer Coefficients (HTC) Correlations and view the section Churchill-Bernstein (Cylinder in Cross Flow).

Table 2. Output List
Index	.flo label	Description
1	TNET	Thermal network ID which has the convector where this correlation is used.
2	CONV_ID	Convector ID which is using this correlation.
3	SHAPE	Shape of the body in cross flow.
4	CHAR_LEN	Characteristic length.
5	OUTER_R	Only appears if RPM Based velocity type is selected. Displays the value of outer radius used in the calculations.
6	TIP_SPD_RATIO	Only appears if RPM Based velocity type is selected. Displays the value of tip speed ratio used in the calculations.
7	VELOCITY	The velocity used in the calculations.
8	PR	Prandtl number.
9	RE	Reynolds number.
10	NU	Calculated Nusselt number.
11	HTC	Calculated heat transfer coefficient.

Heat Transfer Correlation References

Petit J.P., Transfert de chaleur et de masse, Cours de l’Ecole Centrale de Paris.
Incropera, F. and Dewitt, D. Fundamentals of Heat and Mass Transfer, 6th Edition, John Wiley & Sons, 2006.
Jakob, M., Heat Transfer, Vol. 1, Wiley, New York, 1949.