Overview
Since version 2022, Flow Simulator has used the compressibility factor,
z, to adjust the ideal gas relationship for density. The compressibility factor
improves the accuracy for fluids that are at pressures and temperatures where they
do not behave like an ideal gas.
ρ
=
P
z
R
T
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaHbpGCcqGH9aqpdaWcaaWdaeaapeGaamiuaaWdaeaapeGaamOE
aiaacckacaWGsbGaaiiOaiaadsfaaaaaaa@3EF8@
In version 2025, Flow Simulator has an improved accuracy option for
fluids that do not behave as an ideal gas. This new approach uses modified exponents
for the isentropic equations, reference 1. It still uses the compressibility factor
as before. As before, only fluids using Coolprop can model the real gas effects.
From the Material Editor, select the
Real Gas Gamma
option.
Figure 1 . Equations
The two new “gammas” used for real gas:
γ
P
v
=
C
p
P
C
v
β
=
γ
i
d
e
a
l
P
β
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaHZoWzpaWaaSbaaSqaa8qacaWGqbGaamODaaWdaeqaaOWdbiab
g2da9maalaaapaqaa8qacaWGdbWdamaaBaaaleaapeGaamiCaaWdae
qaaaGcbaWdbiaadcfacaGGGcGaam4qa8aadaWgaaWcbaWdbiaadAha
a8aabeaak8qacaGGGcGaeqOSdigaaiabg2da9maalaaapaqaa8qacq
aHZoWzpaWaaSbaaSqaa8qacaWGPbGaamizaiaadwgacaWGHbGaamiB
aaWdaeqaaaGcbaWdbiaadcfacaGGGcGaeqOSdigaaaaa@4FE0@
γ
T
v
=
1
+
v
α
C
v
β
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaHZoWzpaWaaSbaaSqaa8qacaWGubGaamODaaWdaeqaaOWdbiab
g2da9iaaigdacqGHRaWkdaWcaaWdaeaapeGaamODaiabeg7aHbWdae
aapeGaam4qa8aadaWgaaWcbaWdbiaadAhaa8aabeaak8qacaGGGcGa
eqOSdigaaaaa@448E@
α
=
1
v
∂
v
∂
T
P
=
i
s
o
b
a
r
i
c
e
x
p
a
n
s
i
o
n
c
o
e
f
f
i
c
i
e
n
t
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaHXoqycqGH9aqpdaWcaaWdaeaapeGaaGymaaWdaeaapeGaamOD
amaabmaapaqaa8qadaWcaaWdaeaapeGaeyOaIyRaamODaaWdaeaape
GaeyOaIyRaamivaaaaaiaawIcacaGLPaaapaWaaSbaaSqaa8qacaWG
qbaapaqabaaaaOWdbiabg2da9iaadMgacaWGZbGaam4Baiaadkgaca
WGHbGaamOCaiaadMgacaWGJbGaaiiOaiaadwgacaWG4bGaamiCaiaa
dggacaWGUbGaam4CaiaadMgacaWGVbGaamOBaiaacckacaWGJbGaam
4BaiaadwgacaWGMbGaamOzaiaadMgacaWGJbGaamyAaiaadwgacaWG
UbGaamiDaaaa@601A@
β =
− 1
v
∂ v
∂ p
T
= i s o t h e r m a l c o m p r e s s i b i l i t y f a c t o r
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaHYoGycqGH9aqpdaWcaaWdaeaapeGaeyOeI0IaaGymaaWdaeaa
peGaamODamaabmaapaqaa8qadaWcaaWdaeaapeGaeyOaIyRaamODaa
WdaeaapeGaeyOaIyRaamiCaaaaaiaawIcacaGLPaaapaWaaSbaaSqa
a8qacaWGubaapaqabaaaaOWdbiabg2da9iaadMgacaWGZbGaam4Bai
aadshacaWGObGaamyzaiaadkhacaWGTbGaamyyaiaadYgacaGGGcGa
am4yaiaad+gacaWGTbGaamiCaiaadkhacaWGLbGaam4Caiaadohaca
WGPbGaamOyaiaadMgacaWGSbGaamyAaiaadshacaWG5bGaaiiOaiaa
dAgacaWGHbGaam4yaiaadshacaWGVbGaamOCaaaa@6431@
For a fluid near the ideal gas conditions, the two new gammas are equivalent to the
ideal gas gamma.
γ
=
γ
P
v
=
γ
T
v
=
C
p
C
v
,
for ideal gas conditions
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaHZoWzcqGH9aqpcqaHZoWzpaWaaSbaaSqaa8qacaWGqbGaamOD
aaWdaeqaaOWdbiabg2da9iabeo7aN9aadaWgaaWcbaWdbiaadsfaca
WG2baapaqabaGcpeGaeyypa0ZaaSaaa8aabaWdbiaadoeapaWaaSba
aSqaa8qacaWGWbaapaqabaaakeaapeGaam4qa8aadaWgaaWcbaWdbi
aadAhaa8aabeaaaaGcpeGaaiiOaiaacYcacaGGGcGaaeOzaiaab+ga
caqGYbGaaeiOaiaabMgacaqGKbGaaeyzaiaabggacaqGSbGaaeiOai
aabEgacaqGHbGaae4CaiaabckacaqGJbGaae4Baiaab6gacaqGKbGa
aeyAaiaabshacaqGPbGaae4Baiaab6gacaqGZbaaaa@611D@
The isentropic relations and the flow function equations can be rewritten using the
new “gammas”.
P
o
P
=
1
+
γ
P
v
−
1
2
M
2
γ
P
v
γ
P
v
−
1
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qadaWcaaWdaeaapeGaamiua8aadaWgaaWcbaWdbiaad+gaa8aabeaa
aOqaa8qacaWGqbaaaiabg2da9maabmaapaqaa8qacaaIXaGaey4kaS
YaaSaaa8aabaWdbiaacckacqaHZoWzpaWaaSbaaSqaa8qacaWGqbGa
amODaaWdaeqaaOWdbiabgkHiTiaaigdaa8aabaWdbiaaikdaaaGaam
yta8aadaahaaWcbeqaa8qacaaIYaaaaaGccaGLOaGaayzkaaWdamaa
CaaaleqabaWdbmaalaaapaqaa8qacaGGGcGaeq4SdC2damaaBaaame
aapeGaamiuaiaadAhaa8aabeaaaSqaa8qacaGGGcGaeq4SdC2damaa
BaaameaapeGaamiuaiaadAhaa8aabeaal8qacqGHsislcaaIXaaaaa
aaaaa@538E@
T
o
T
=
1
+
γ
P
v
−
1
2
M
2
γ
T
v
−
1
γ
P
v
−
1
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qadaWcaaWdaeaapeGaamiva8aadaWgaaWcbaWdbiaad+gaa8aabeaa
aOqaa8qacaWGubaaaiabg2da9maabmaapaqaa8qacaaIXaGaey4kaS
YaaSaaa8aabaWdbiaacckacqaHZoWzpaWaaSbaaSqaa8qacaWGqbGa
amODaaWdaeqaaOWdbiabgkHiTiaaigdaa8aabaWdbiaaikdaaaGaam
yta8aadaahaaWcbeqaa8qacaaIYaaaaaGccaGLOaGaayzkaaWdamaa
CaaaleqabaWdbmaalaaapaqaa8qacaGGGcGaeq4SdC2damaaBaaame
aapeGaamivaiaadAhaa8aabeaal8qacqGHsislcaaIXaaapaqaa8qa
caGGGcGaeq4SdC2damaaBaaameaapeGaamiuaiaadAhaa8aabeaal8
qacqGHsislcaaIXaaaaaaaaaa@5561@
m
˙
T
o
P
o
A
=
γ
P
v
z
o
R
M
1
+
γ
P
v
−
1
2
M
2
γ
P
v
+
1
2
γ
P
v
−
1
MathType@MTEF@5@5@+=
feaahGart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qadaWcaaWdaeaapeGabmyBa8aagaGaa8qadaGcaaWdaeaapeGaamiv
a8aadaWgaaWcbaWdbiaad+gaa8aabeaaa8qabeaaaOWdaeaapeGaam
iua8aadaWgaaWcbaWdbiaad+gaa8aabeaak8qacaWGbbaaaiabg2da
9maalaaapaqaa8qadaGcaaWdaeaapeWaaSaaa8aabaWdbiabeo7aN9
aadaWgaaWcbaWdbiaadcfacaWG2baapaqabaaakeaapeGaamOEa8aa
daWgaaWcbaWdbiaad+gaa8aabeaak8qacaWGsbaaaaWcbeaakiaacc
kacaWGnbaapaqaa8qadaqadaWdaeaapeGaaGymaiabgUcaRmaalaaa
paqaa8qacaGGGcGaeq4SdC2damaaBaaaleaapeGaamiuaiaadAhaa8
aabeaak8qacqGHsislcaaIXaaapaqaa8qacaaIYaaaaiaad2eapaWa
aWbaaSqabeaapeGaaGOmaaaaaOGaayjkaiaawMcaa8aadaahaaWcbe
qaa8qadaWcaaWdaeaapeGaeq4SdC2damaaBaaameaapeGaamiuaiaa
dAhaa8aabeaal8qacqGHRaWkcaaIXaaapaqaa8qacaaIYaWaaeWaa8
aabaWdbiabeo7aN9aadaWgaaadbaWdbiaadcfacaWG2baapaqabaWc
peGaeyOeI0IaaGymaaGaayjkaiaawMcaaaaaaaaaaaaa@62E0@
For a fluid near the ideal gas conditions, these equations are equivalent to the
ideal gas equations.
Output
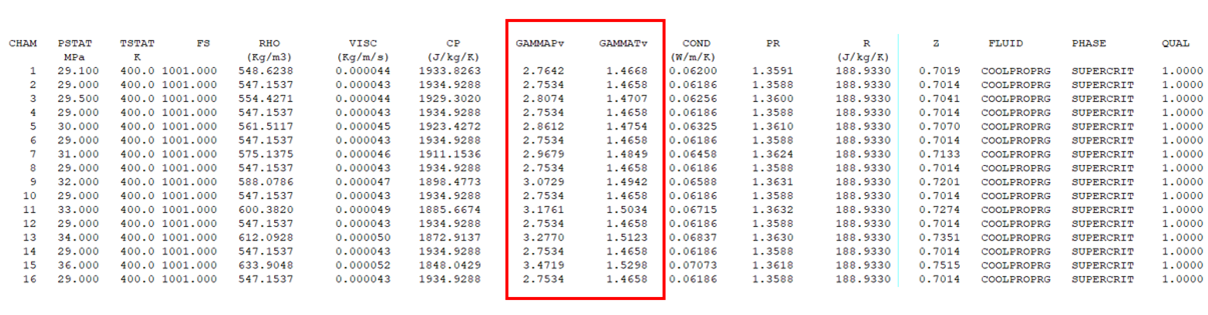
The *.
prop file has a column for these two new “gammas”. The
“RG” at the end of “COOLPROPRG” in the output files also denotes the real gas gammas
that were used in the analysis.
Figure 2 .