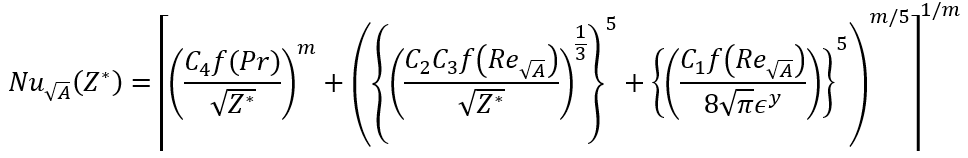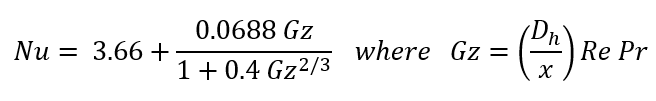Heat Transfer Coefficients (HTC) Correlations

The following sections describe the available heat transfer correlations (HTCs) in Flow Simulator. Correlation equations and literature references are included. All HTC options appear in the 1D-Thermal Convection Resistor. In addition, the duct flow HTC options appear in the Tube/Pipe flow elements and the Advance Orifice flow element.


Nomenclature:	Subscripts:
Nu: Nusselt Number	lam: Laminar Regime
Re: Reynolds number	turb: Turbulent Regime
Pr: Prandtl multiplier	tran: Transition Regime
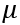: Dynamic Viscosity

Heat Transfer Correlations:

Lapides-Goldstein:

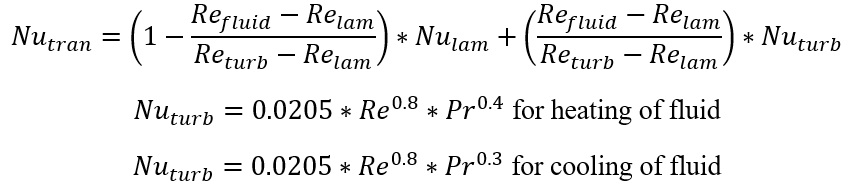
Dittus-Boelter:

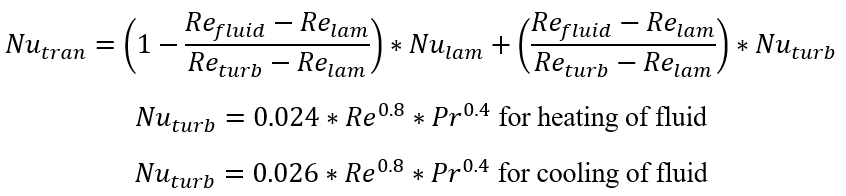
Sieder-Tate:

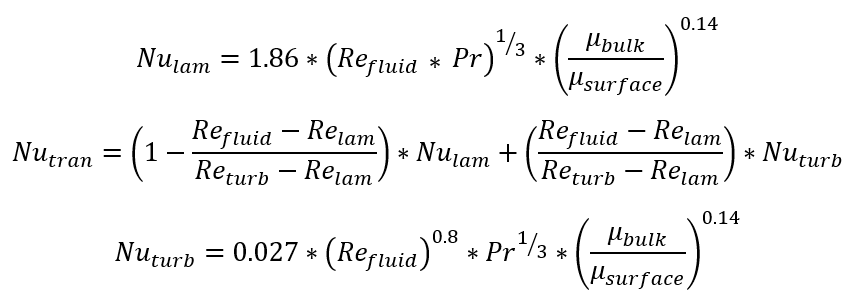
Gnielinski:

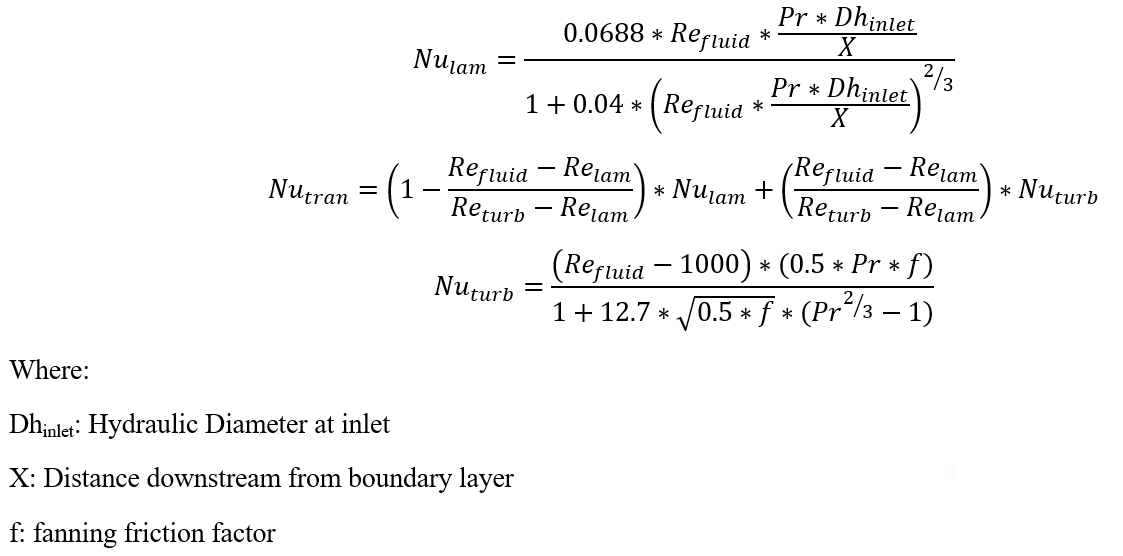
Bhatti-Shah:

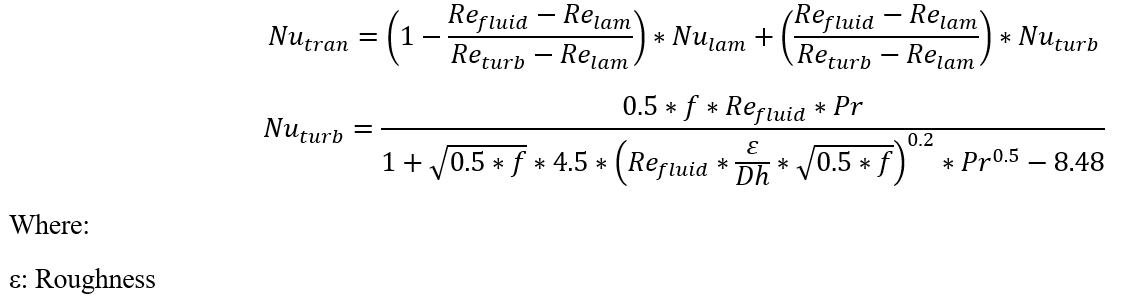
External Heat Transfer:

The following section lists cross flow convection and free convection configurations that are available in Flow Simulator. These options are primarily used by connecting a 1D Thermal Convection Resistor to an internal chamber in the flow path.

Colburn (Plate in Cross Flow):

Incropera (Plate in Cross Flow)

The flat plate correlation based on Incropera (reference 4) calculates an average Nusselt number for the laminar flow over the entire plate, or the mixed laminar and turbulent flow over the plate. The plate is assumed to have a constant surface temperature.

For Re < ~500,000:

N u_{a v e r a g e_l a m i n a r} = 0.664 * {(\frac{ρ * V * L}{μ})}^{0.5} * P r^{0.333}

For Re > ~500,000:

N u_{a v e r a g e_m i x} = [0.037 * {(\frac{ρ * V * L}{μ})}^{0.8} - 871.0] * P r^{0.333}

Where:

$L = P l a t e l e n g t h i n c r o s s f l o w d i r e c t i o n$

$V = f l u i d c r o s s f l o w v e l o c i t y$

$ρ = f l u i d f i l m d e n s i t y$

$μ = f l u i d f i l m v i s c o s i t y$

P r = f l u i d P r a n d t l N u m b e r

Note: Valid for 10 < Re < 10⁸, Pr > 0.6

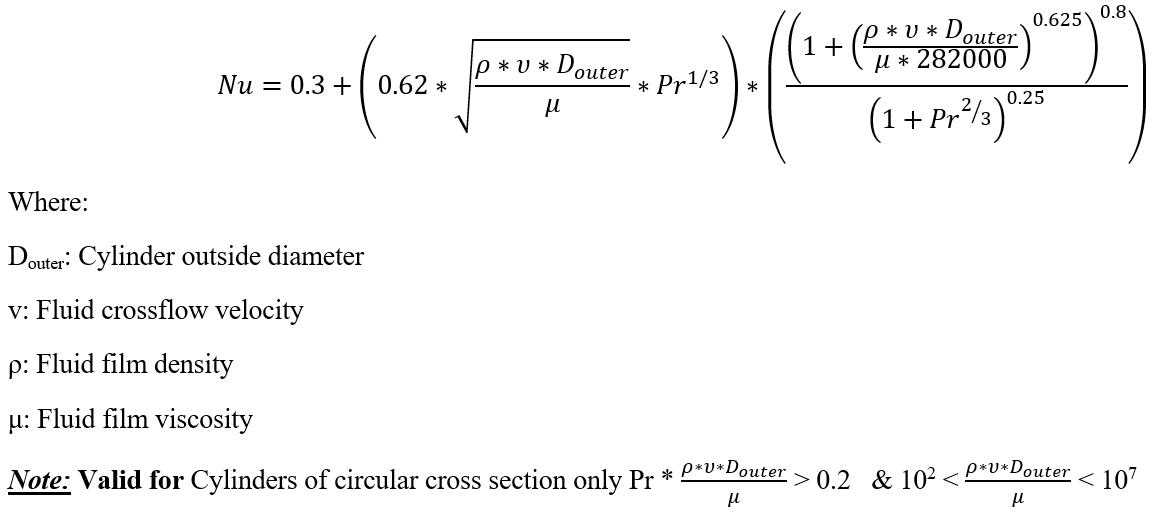
Churchill-Bernstein (Cylinder in Cross Flow):

McAdams (Vertical Prism in Free Convection):

Horizontal Plate in Free Convection:

Churchill-Chu(Horizontal Cylinder in Free Convection):

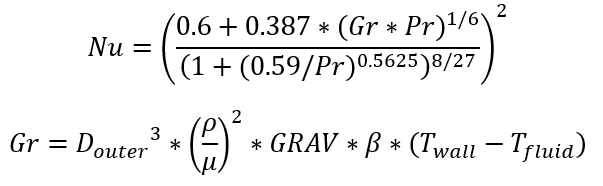
Where:

Gr: Grashof number

D_outer: Cylinder outside diameter

ρ: Fluid bulk density

μ: Fluid film viscosity

GRAV: Earth Gravity

β: Fluid bulk compressibility factor

Note: Valid for 10⁶ < (Gr*Pr) < 10¹²

Turbulent Duct Flow Entrance Effects

The following entrance effects correlations compute an HTC multiplier called Hm. HTC multiplier has limits and must be greater than unity. The Local option resolves heat transfer correctly for all x locations along the axial length of a pipe. The Averaged options use total pipe length L as the input. They correctly predict overall heat transfer, but not local temperature variation.

Abrupt Contraction, Local x

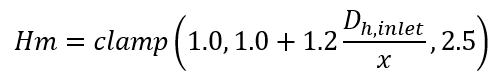
Uniform Bellmouth, Local x

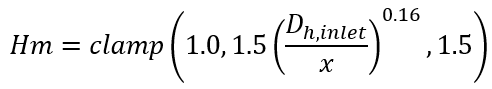
Abrupt Contraction, Averaged L

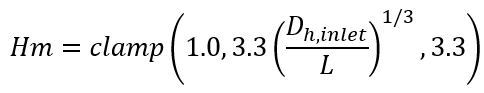
Uniform Bellmouth, Averaged L

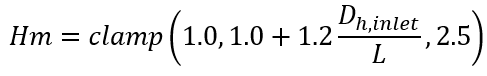
Uniform Blend, Local x

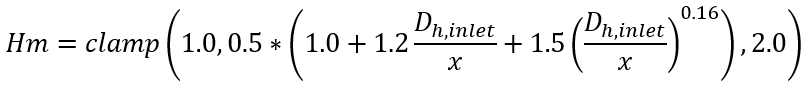
Uniform Blend, Averaged L

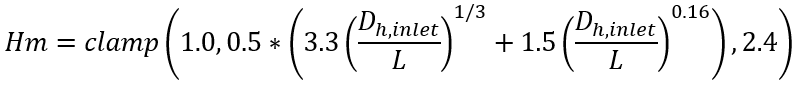
Laminar Duct Flow HTC correlations

The following Laminar HTC options are available in Flow Simulator. It is worth noting that Laminar HTCs depend on distance from inlet x, and thus do not need a special Entrance Effects multiplier.

Muzychka-Yovanovich:

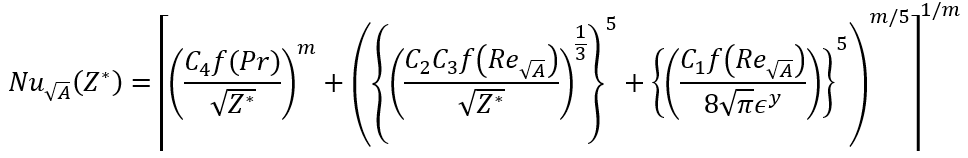
Hausen:
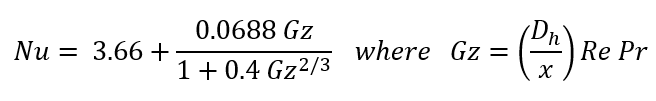
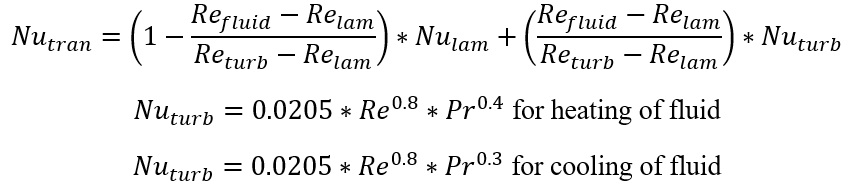
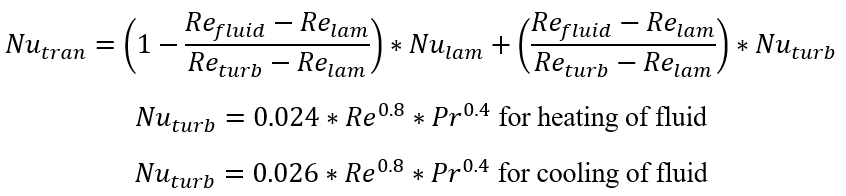
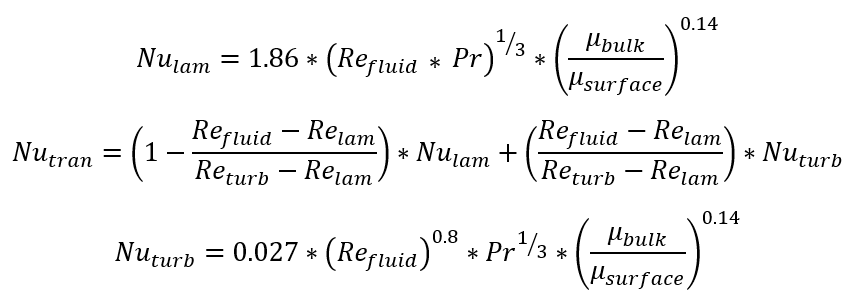
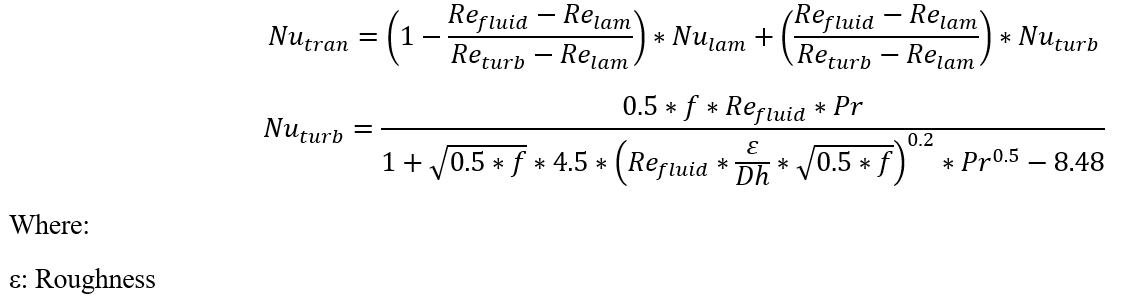
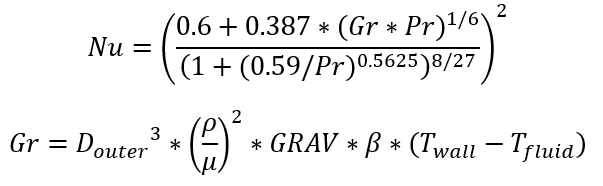
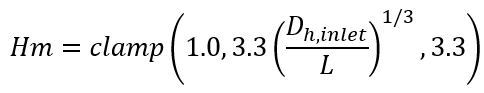