Gaz properties

Introduction

Here is the process to define and fit the gas thermal characteristics from the importation of a series of points representing the considered quantity curve listed in an Excel file. In the following example air mass density is considered; however, the same principle is applied for all other gas properties depending on temperature, which are defined below.

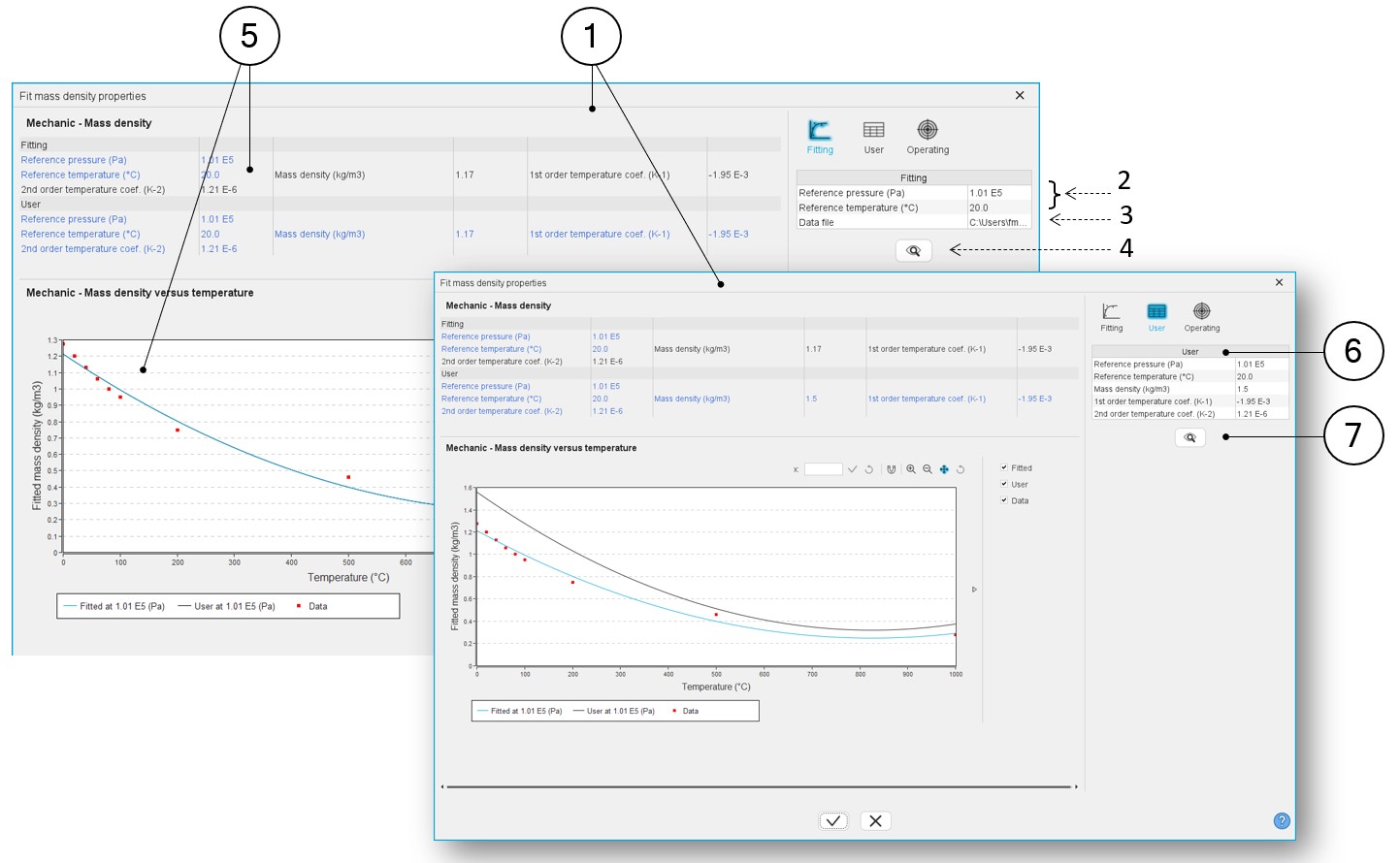Table 1. Identification of the air mass density curve characteristics (for instance)


1 Dialog box allowing the characterization of the density curve imported from an Excel file
2 Select the reference conditions (temperature and pressure) associated with the measures contained in the Excel file.
3 Path where the Excel file containing the measures is stored. See an example of Excel file below.
4 Click on this button to import the Excel data.
5 When importing an Excel file, points representing the density curve are listed, and an optimization process automatically computes and displays the corresponding characteristics.
Three curves are displayed:
  • Red points are the imported points (listed in the Excel file)
  • The blue curve is the resulting curve computed by the optimization process. This corresponds to the computed characteristics and it is displayed just after the computation.
  • The black curve shows a new curve generated when the parameters are changed by the user (see point 6)
6 Indeed, going to the tab “User”, the user can adjust one or all the main parameters of the density curve.
  • The density at reference temperature
  • The density first order temperature coefficient
  • The density second order temperature coefficient

Reference temperature and pressure can also be adjusted in this tab.
7 It is possible to select an operating pressure to visualize the behavior of the resulting mass density curve. Operating pressure should be chosen in the “Operating” tab.
Note: If the chosen pressure is not the same as the one used for the fitting process, the measurement points (in red) will not be displayed.

Example of an Excel file to define the mass density curve parameters.

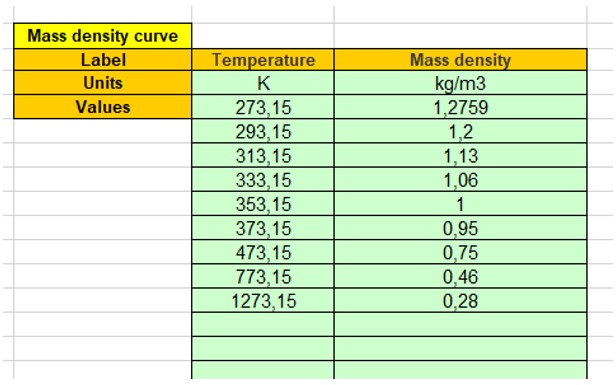
Figure 1. Example of an Excel file to define the air mass density curve parameters


Note: An Excel file “airMassDensity.xls” can be found in the folder …\FluxMotor\Resources\DefaultFiles\Templates\Materials.

It allows to see what the correct format is to be applied for filling the data.

Mass density



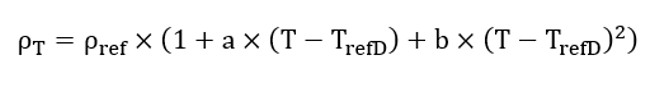
Symbol Definition Unit
P ref Reference pressure Pa
T refD Mass density reference temperature T refD °C
r ref Mass density at T refD and P ref kg/m3
a Mass density first order temperature coefficient at T refD and P ref K-1
b Mass density second order temperature coefficient at T refD and P ref K-2
Note: The reference pressure mentioned in the previous table is the one considered for defining the gas specific heat.
Note: For a given temperature, the gas density (kg/m3) changes with the pressure following the perfect gas law.

The mass density ρ computed at a pressure P is computed as below:



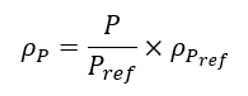
Dynamic viscosity



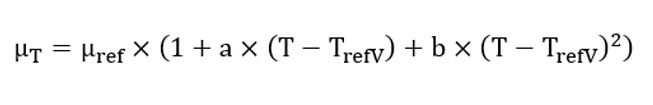
Symbol Definition Unit
T refV Dynamic viscosity reference temperature °C
μref Dynamic viscosity at T refV kg/m/s
a Dynamic viscosity first order temperature coefficient at T refV K-1
b Dynamic viscosity second order temperature coefficient at T refV K-2
Note: The model does not consider any variation of the gas dynamic viscosity with the gas pressure.

Thermal conductivity



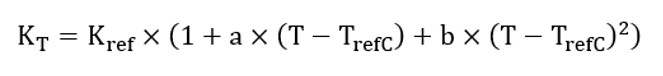
Symbol Definition Unit
T refC Thermal conductivity reference temperature °C
K ref Thermal conductivity at T refC W/K/m
a Thermal conductivity first order temperature coefficient at T refC K-1
b Thermal conductivity second order temperature coefficient at T refC K-2
Note: The model does not consider any variation of the gas thermal conductivity in function with the gas pressure.

Specific heat



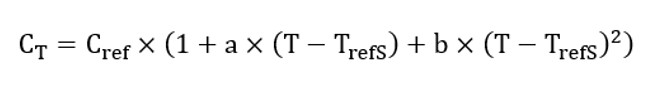
Symbol Definition Unit
T refS Specific heat reference temperature °C
C ref Specific heat at T refS and P ref J/K/Kg
a Specific heat first order temperature coefficient at T refS and P ref (K-1) K-1
b Specific heat second order temperature coefficient at T refS and P ref (K-2) K-2
Note: All the parameters defined in the previous table are defined for the reference pressure Pref mentioned in the gas mass density section.
Note: For a given temperature, the gas specific heat (J/K/kg) changes with the pressure following the perfect gas law.

The specific heat C computed at a pressure P is computed as below:



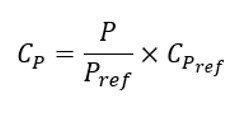
Symbol Definition Unit
P ref Reference pressure Pa
C P Specific heat at the pressure P J/K/Kg
C Pref Specific heat at the pressure P ref J/K/Kg