/MAT/LAW127 (ENHANCED_COMPOSITE)

Block Format Keyword The model may be used to model composite materials with unidirectional layers. This model is implemented only for shell, thick shell and solid elements.

Format


(1)	(2)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW127/`mat_ID`/`unit_ID` or /MAT/ENHANCED_COMPOSITE/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`₁₁		`E`₂₂	`E`₃₃
`G`₁₂		`G`₁₃	`G`₂₃
$ν_{21}$		$ν_{31}$	$ν_{32}$
$σ_{T 1}$		`SLIM`_T1		`Fct_ID`_T1	`Fscale`_T1
$σ_{T 2}$		`SLIM`_T2		`Fct_ID`_T2	`Fscale`_T2
$σ_{S}$		`SLIM`_S		`Fct_ID`_S	`Fscale`_S
$σ_{C 1}$		`SLIM`_C1		`Fct_ID`_C1	`Fscale`_C1
$σ_{C 2}$		`SLIM`_C2		`Fct_ID`_C2	`Fscale`_C2
`Fcut`
$α$		$β$	`2WAY`	`TI`
`DFAILT`		`DFAILC`	`DFAILS`		`DFAILM`	`RATIO`
	`NCYRED`		`FBRT`		`YCFAC`
`EFS`		`EPSF`	`EPSR`		`TSMD`

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`₁₁	Young’s modulus in fiber, longitudinal direction 1. (Real)	$[Pa]$
`E`₂₂	Young’s modulus in matrix, transverse direction 2. (Real)	$[Pa]$
`E`₃₃	Young’s modulus in matrix, normal direction 3. (Real)	$[Pa]$
`G`₁₂	Shear modulus 12. (Real)	$[Pa]$
`G`₁₃	Shear modulus 13. (Real)	$[Pa]$
`G`₂₃	Shear modulus 23. (Real)	$[Pa]$
$ν_{21}$	Poisson’s ratio 21. (Real)
$ν_{31}$	Poisson’s ratio 31. (Real)
$ν_{32}$	Poisson’s ratio 32. (Real)
$σ_{T 1}$	Maximum tensile stress in direction 1. Ignore if `Fct_ID`_T1 is defined. Default = 1E+20 (Real)
`SLIM`_T1	Factor to determine the minimum stress limit after stress maximum $σ_{T 1}$ is reached. 2 Default = 1.0 (Real)
`Fct_ID`_T1	Load curve identifier defining the tensile stress in direction 1 $σ_{T 1}$ as a function of strain rate. (Integer)
`Fscale`_T1	Stress scale factor for the function `Fct_ID`_T1. Default = 1.0 (Real)	$[Pa]$
$σ_{T 2}$	Maximum tensile stress in direction 2. Ignore if `Fct_ID`_T2 is defined. Default = 1E+20 (Real)
`SLIM`_T2	Factor to determine the minimum stress limit after stress maximum $σ_{T 2}$ . 2 Default = 1.0 (Real)
`Fct_ID`_T2	Load curve identifier defining the tensile stress in direction 1 $σ_{T 2}$ as a function of strain rate. (Integer)
`Fscale`_T2	Stress scale factor for the function `Fct_ID`_T2. Default = 1.0 (Real)	$[Pa]$
$σ_{S}$	Maximum shear stress in plane 12. Ignore if `Fct_ID`_S is defined. Default = 1E+20 (Real)
`SLIM`_S	Factor to determine the minimum stress limit after stress maximum $σ_{S}$ . 2 Default = 1.0 (Real)
`Fct_ID`_S	Load curve ID defining the shear stress in plane 12. $σ_{S}$ as a function of strain rate. (Integer)
`Fscale`_S	Stress scale factor for the function `Fct_ID`_S. Default = 1.0 (Real)	$[Pa]$
$σ_{C 1}$	Maximum compression stress in direction 1. Ignore if `Fct_ID`_C1 is defined. Default = 1E+20 (Real)
`SLIM`_C1	Factor to determine the minimum stress limit after stress maximum $σ_{C 1}$ is reached. 2 Default = 1.0 (Real)
`Fct_ID`_C1	Load curve identifier defining the compression stress in direction 1 $σ_{C 1}$ as a function of strain rate. (Integer)
`Fscale`_C1	Stress scale factor for the function `Fct_ID`_C1. Default = 1.0 (Real)	$[Pa]$
$σ_{C 2}$	Maximum compression stress in direction 2. Ignore if `Fct_ID`_C2 is defined. Default = 1E+20 (Real)
`SLIM`_C2	Factor to determine the minimum stress limit after stress maximum $σ_{C 2}$ is reached. 2 Default = 1.0 (Real)
`Fct_ID`_C2	Load curve identifier defining the compression stress in direction 1 $σ_{C 2}$ as a function of strain rate. (Integer)
`Fscale`_C2	Stress scale factor for the function `Fct_ID`_C2. Default = 1.0 (Real)	$[Pa]$
`Fcut`	Equivalent strain rate cutoff frequency. Default = 5000 Hz (Real)	$[\frac{1}{s}]$
$α$	Shear stress parameter for the nonlinear term. 3 Default = 0.0 (Real)
$β$	Weighing factor for shear term in tensile fiber mode. 3 0.0 ≤ $β$ ≤ 1.0 Default = 0.0 (Real)
`2WAY`	Flag to turn on 2-way fiber action. This option is available only for solid and thick shells. = 0 (Default) Standard unidirectional behavior, meaning fibers run only in the direction 1. = 1 2-way fiber behavior, meaning fibers run in both the first and second directions. The meaning of the fields `DFAILT`, `DFAILC`, `YC`, `YT`, `SLIM`_T2 and `SLIM`_C2 are altered if this flag is set. (Integer)
`TI`	Flag to turn on transversal isotropic behavior for material solid elements. 7 = 0 (Default) Standard unidirectional behavior = 1 Transversal isotropic behavior (Integer)
`DFAILT`	Maximum strain for fiber tension. 5 If `2WAY` =1, then `DFAILT` is the fiber tensile failure strain in the first and second directions. Default = 1E+10 (Real)
`DFAILC`	Maximum strain for fiber compression (active only if `DFAILT` > 0). The input value should be negative. 5 Default = -1E+10 (Real)
`DFAILS`	Maximum tensorial shear strain (active only if `DFAILT` > 0). 5 Default = 1E+10 (Real)
`DFAILM`	Maximum strain for matrix straining in tension or compression (active only if `DFAILT` > 0). 5 Default = 1E+10 (Real)
`RATIO`	Ratio parameter control to delete shell elements. Defines a ratio of failed plies in thickness. Default = 1.0 (Real)
`NCYRED`	Number of cycles for stress reduction from maximum to minimum. Default = 1 (Integer)
`FBRT`	Softening factor for fiber tensile stress: = 0.0 Tensile stress is $σ_{T 1}$ . > 1.0 Tensile strength is $σ_{T 1}$ reduced by `FBRT` after failure occurred in compressive matrix mode. Default = 1.0 (Real)
`YCFAC`	Reduction factor for compressive fiber stress after matrix compressive failure. The compressive stress in the fiber direction $σ_{1}^{c}$ is reduced by `YCFAC` after compressive matrix failure. Default = 2.0 (Real)
`EFS`	Maximum effective strain for element layer failure. 5 Default = 1E+10 (Real)
`EPSF`	Damage initiation transverse shear strain. 6 Default = 1E+10 (Real)
`EPSR`	Final rupture transverse shear strain. 6 Default = 2E+10 (Real)
`TSMD`	Transverse shear maximum damage. 6 Default = 0.90 (Real)

Example (Composite)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
Unit for material
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW127/1
Composite
#        Init. dens.
             1.5E-09
#                E11                 E22                 E33
             15000.0             15000.0             15000.0
#                G12                 G13                 G23
              5000.0              1000.0              1000.0
#               Nu21                Nu31                Nu32
                 0.1                 0.1                 0.1
#             SIG_T1             SLIM_T1           FCT_ID_T1           FSCALE_T1
               400.0                0.25                   0                 0.0
#             SIG_T2             SLIM_T2           FCT_ID_T2           FSCALE_T2
               400.0                0.25                   0                 0.0
#              SIG_S              SLIM_S            FCT_ID_S            FSCALE_S
                50.0                 1.0                   0                 0.0
#             SIG_C1             SLIM_C1           FCT_ID_C1           FSCALE_C1
               200.0                 0.5                   0                 0.0
#             SIG_C2             SLIM_C2           FCT_ID_C2           FSCALE_C2
               200.0                 0.5                   0                 0.0
#               FCUT
                 0.0
#               ALPH                BETA      2WAY        TI
                 0.0                 0.0         0         0
#             DFAILT              DFAILC              DFAILS              DFAILM               RATIO
                0.05                -0.2                 0.2                 0.3                 0.0
#             NCYRED                                    FBRT               YCFAC
                  10                                     0.0                 0.0
#                EFS                EPSF                EPSR                TSMD
                 0.2                 0.5                 0.8                 1.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

This material model presents linear elastic behavior until failure. Pseudo-plastic behavior is implemented as post-failure behavior until reaching a strain criterion controlling the ultimate material failure:
- Under 2D stress conditions, for shells, the stress/strain relationship in the orthotropic frame is given by:
  $\{\begin{cases} σ_{11} = C_{11} ε_{11} + C_{12} ε_{22} \\ σ_{22} = C_{21} ε_{11} + C_{22} ε_{22} \\ σ_{12} = G_{12} ε_{12} \\ σ_{23} = κ G_{23} ε_{23} \\ σ_{31} = κ G_{13} ε_{31} \end{cases}$
  Where,
  
  $C = \frac{1}{1 - ν_{12} ν_{21}} [\begin{matrix} E_{11} & ν_{12} E_{22} \\ ν_{21} E_{11} & E_{22} \end{matrix}]$
  
  $κ$
  
  Out of plane shear coefficient scale factor
- The 3D stress/strain relationship in the orthotropic frame is given by:
  $\{\begin{cases} σ_{11} = C_{11} ε_{11} + C_{12} ε_{22} + C_{13} ε_{33} \\ σ_{22} = C_{12} ε_{11} + C_{22} ε_{22} + C_{23} ε_{33} \\ σ_{33} = C_{13} ε_{11} + C_{23} ε_{22} + C_{33} ε_{33} \\ σ_{12} = G_{12} ε_{12} \\ σ_{23} = G_{23} ε_{23} \\ σ_{31} = G_{13} ε_{31} \end{cases}$
  Where, $C = \frac{1}{1 - ν_{12} ν_{21} - ν_{13} ν_{31} - ν_{23} ν_{32} - 2 ν_{21} ν_{32} ν_{13}} [\begin{matrix} E_{1} (1 - ν_{23} ν_{32}) & E_{11} [ν_{21} - ν_{31} ν_{32}] & E_{11} [ν_{31} - ν_{21} ν_{32}] \\ s y m & E_{2} (1 - ν_{13} ν_{31}) & E_{22} [ν_{32} - ν_{12} ν_{31}] \\ s y m & s y m & E_{3} (1 - ν_{12} ν_{21}) \end{matrix}]$
Pseudo-Plastic behavior is considered at the post failure behavior for each direction:
Figure 1. Behavior in direction 1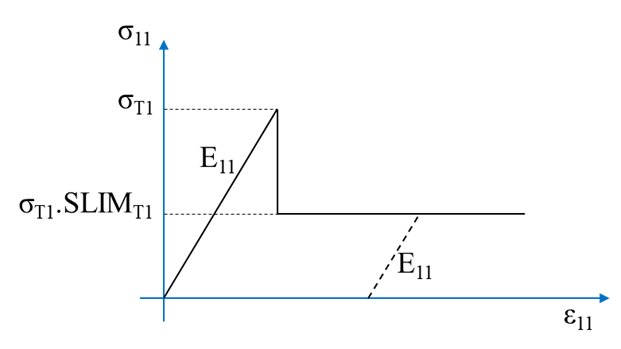
The Chang-Chang criteria are given as:
- Tensile Fiber mode:
  $σ_{11} > 0 \Rightarrow e_{f}^{2} = {(\frac{σ_{11}}{σ_{T 1}})}^{2} + β {(\frac{σ_{12}}{σ_{S}})}^{2} - 1 \Rightarrow \{\begin{cases} e_{f}^{2} \geq 0 failed \\ e_{f}^{2} < 0 elastic \end{cases}$
  If $e_{f}^{2} \geq 0$ , shell element ply is removed if DFAILT =0 or solid element is deleted.
- Compressive Fiber mode:
  $σ_{11} < 0 \Rightarrow e_{f}^{2} = {(\frac{σ_{11}}{σ_{C 1}})}^{2} - 1 \Rightarrow \{\begin{cases} e_{f}^{2} \geq 0 failed \\ e_{f}^{2} < 0 elastic \end{cases}$
  If $e_{f}^{2} \geq 0$ , $σ_{11}$ is set to minimum stress limit.
- Tensile Matrix mode:
  $σ_{22} > 0 \Rightarrow e_{m}^{2} = {(\frac{σ_{22}}{σ_{T 2}})}^{2} + (\frac{\frac{σ_{12}^{2}}{2 G_{12}} + \frac{4}{3} \cdot α \cdot σ_{12}^{4}}{\frac{σ_{S}^{2}}{2 G_{12}} + \frac{4}{3} \cdot α \cdot σ_{S}^{4}}) - 1 \Rightarrow \{\begin{cases} e_{m}^{2} \geq 0 failed \\ e_{m}^{2} < 0 elastic \end{cases}$
  If $e_{m}^{2} \geq 0$ , $σ_{22}$ is set to minimum stress limit.
- Compressive Matrix mode:
  $σ_{22} < 0 \Rightarrow e_{m}^{2} = {(\frac{σ_{22}}{σ_{C 2}})}^{2} - 1 \Rightarrow \{\begin{cases} e_{m}^{2} \geq 0 failed \\ e_{m}^{2} < 0 elastic \end{cases}$
  If $e_{m}^{2} \geq 0$ , $σ_{22}$ is set to minimum stress limit.
- The original criterion of Hashin in the tensile fiber mode is set with $β$ = 1.
- For $β$ = 0, you get the maximum stress criterion which is found to compare better to experiments.
If the 2WAY fiber flag is set, then the failure criteria for tensile and compressive fiber failure in the orthotropic 1 direction are unchanged. For orthotropic direction 2, the same failure criteria as for the 1-direction fibers are used:
- Tensile fiber mode in the orthotropic direction 2:
  $σ_{22} > 0 \Rightarrow e_{f}^{2} = {(\frac{σ_{22}}{σ_{T 2}})}^{2} + β {(\frac{σ_{12}}{σ_{S}})}^{2} - 1 \Rightarrow \{\begin{cases} e_{f}^{2} \geq 0 failed \\ e_{f}^{2} < 0 elastic \end{cases}$
  If $e_{f}^{2} \geq 0$ , shell element ply is removed if DFAILT =0 or solid element is deleted.
- Compressive fiber mode in the orthotropic direction 2:
  $σ_{22} < 0 \Rightarrow e_{f}^{2} = {(\frac{σ_{22}}{σ_{C 2}})}^{2} - 1 \Rightarrow \{\begin{cases} e_{f}^{2} \geq 0 failed \\ e_{f}^{2} < 0 elastic \end{cases}$
  If $e_{f}^{2} \geq 0$ , $σ_{22}$ is set to minimum stress limit.
- Matrix fails only in shear:
  $e_{m}^{2} = {(\frac{σ_{12}}{σ_{S}})}^{2} - 1 \Rightarrow \{\begin{cases} e_{m}^{2} \geq 0 failed \\ e_{m}^{2} < 0 elastic \end{cases}$
  If $e_{m}^{2} \geq 0$ , $σ_{12}$ is set to minimum stress limit.
Integration point failure can occur in three different ways:
- If DFAILT is zero, failure occurs if the Chang-Chang failure criterion is satisfied in the tensile fiber mode.
- If DFAILT is greater than zero, failure occurs if:
  - The fiber strain is greater than DFAILT or less than DFAILC
  - If the absolute value of matrix strain is greater than DFAILM
  - If the absolute value of tensorial shear strain is greater than DFAILS
- If EFS is greater than zero, failure occurs if the effective strain is greater than EFS.
Transverse shear strain damage model.
In an optional damage model for transverse shear strain, out-of-plane stiffness (G₁₃ and G₂₃) can linearly decrease to model interlaminar shear failure. Damage starts when effective transverse shear strain $ε_{e f f} = \sqrt{ε_{13}^{2} + ε_{23}^{2}}$ reaches EPSF. Final rupture occurs when effective transverse shear strain reaches EPSR.
A maximum damage of TSMD (0.0 < TSMD < 0.99) cannot be exceeded.
Figure 2. Linear damage for transverse shear behavior
The flag TI applies only to transversal isotropic behavior for material solid elements. the stress/strain relationship is given using the 3D stress/Strain relationship, under the following conditions:
$\begin{array}{l} E_{11} = E_{22} \\ E_{33} \\ ν_{12} = ν_{21} \\ ν_{31} = ν_{32} \\ G_{23} = G_{13} \\ G_{12} = \frac{E_{11}}{2 (1 + ν_{12})} \end{array}$
Damage mode value can be display with the output /H3D/ELEM/DAMG/ID=<mat_ID>/MODE=ALL/… with the following output:
- Tensile fiber damage
- Compressive tensile damage
- Tension transverse matrix damage
- Compressive transverse matrix damage
- Shear matrix damage