HS-2210: Principle Component Analysis of a Cantilever Ibeam

Learn perform a Principle Component Analysis of a cantilever ibeam using a D-Optimal DOE.

Before you begin, copy the model files used in this tutorial from <hst.zip>/HS-2210/ to your working directory.

Perform the Study Setup

  1. Start HyperStudy.
  2. Start a new study in the following ways:
    • From the menu bar, click File > New.
    • On the ribbon, click .
  3. In the Add Study dialog, enter a study name, select a location for the study, and click OK.
  4. Go to the Define Models step.
  5. Add a Parameterized File model.
    1. From the Directory, drag-and-drop the ibeam.tpl file into the work area.
      Figure 1.


    2. In the Solver input file column, enter ibeam.py.
      This is the name of the solver input file HyperStudy writes during any evaluation.
    3. In the Solver execution script column, select Python (py).
  6. Click Import Variables.
    Four input variables are imported from the ibeam.tpl resource file.
  7. Go to the Define Input Variables step.
  8. Review the input variable's lower and upper bound ranges.

Perform Nominal Run

  1. Go to the Test Models step.
  2. Click Run Definition.
    An approaches/setup_1-def/ directory is created inside the study Directory. The approaches/setup_1-def/run__00001/m_1 directory contains the input file, which is the result of the nominal run.

Create and Evaluate Output Responses

  1. Go to the Define Output Responses step.
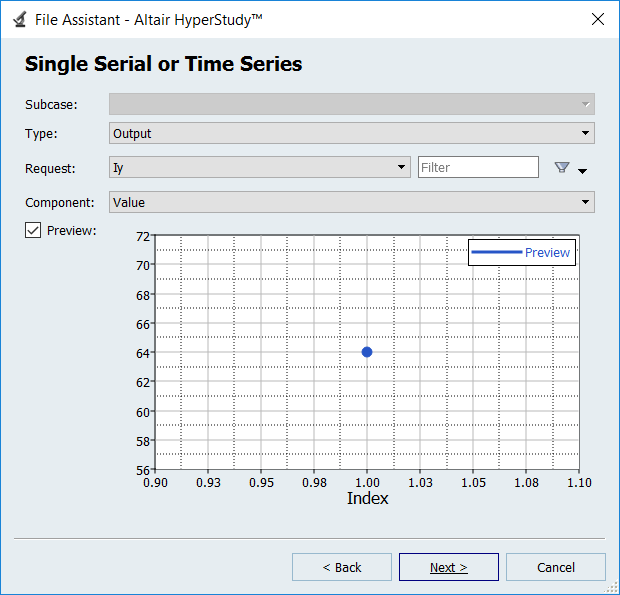
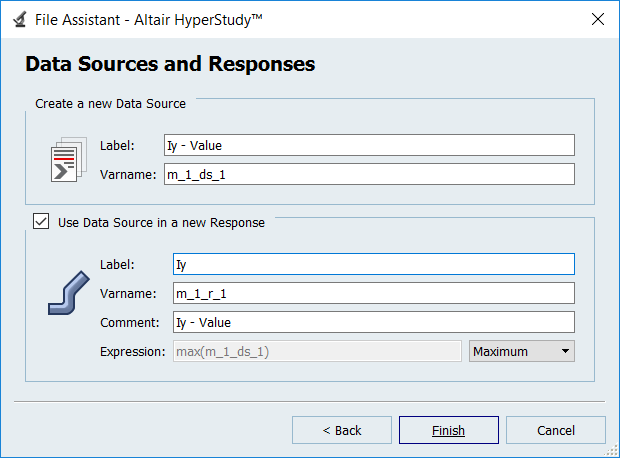
  2. Create the Iy output response for the y-axis moment of inertia.
    1. From the Directory, drag-and-drop the output.hstp file, located in approaches/setup_1-def/run__00001/m_1, into the work area.
    2. In the File Assistant dialog, set the Reading technology to Altair® HyperWorks® and click Next.
    3. Select Single item in a time series, then click Next.
    4. Define the following options, and then click Next.
      • Set Type to Output.
      • Set Request to Iy.
      • Set Component to Value.
      Figure 2.


    5. Label the output response Iy.
    6. Set Expression to Maximum.
    7. Click Finish.
      Figure 3.


  3. Create four more output responses by repeating step 2, except change the Request assigned to each output response to the following:
    Output Response Request
    Volume Vol
    IZ Iz
    Displacement d
    Frequency1 Freq
  4. Click Evaluate to extract the response values.

Run D-Optimal DOE

  1. Add a DOE.
    1. In the Explorer, right-click and select Add from the context menu.
      The Add dialog opens.
    2. From Select Type, choose DOE.
    3. For Definition from, select an approach.
    4. Select Setup and click OK.
  2. Go to the DOE 1 > Specifications step.
  3. In the work area, set the Mode to D-Optimal.
  4. In the Settings tab, change the Number of Runs to 13.
    This is 2 more runs than the minimum required value.
    Figure 4.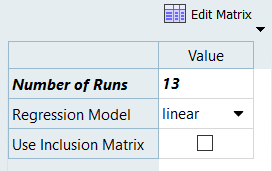


  5. Click Apply.
  6. Go to the DOE 1 > Evaluate step.
  7. Click Evaluate Tasks.
  8. Go to the DOE 1 > Post-Processing step.
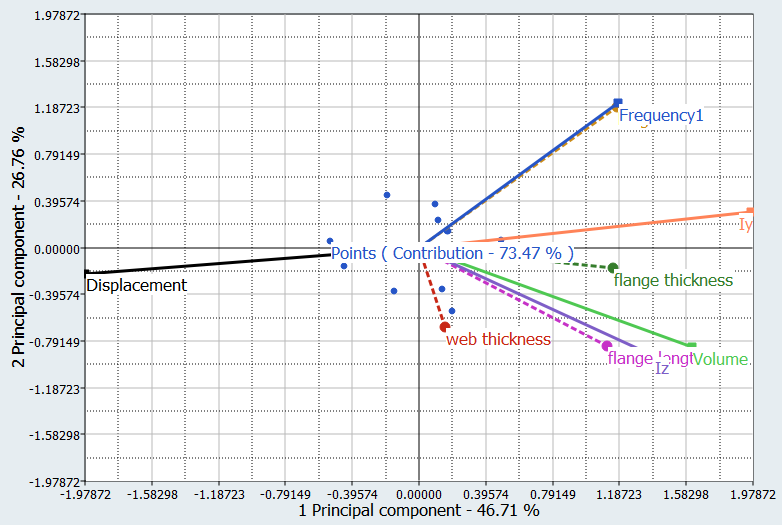
  9. Click the Ordination tab.
    The biplot is interpreted by looking at the relationship between the lines that each represent one input variable or output response. The Displacement and Iy output responses show a strong negative correlation because they are aligned, but pointing in opposite directions. The displacement and Iy are also not at all correlated to the input variable web thickness, indicated by the orthogonality. Similar strong positive correlations are seen between the frequency and height or the volume, Iz, and flange length.
    Figure 5.