HS-2005: DOE Study of a Cantilever Beam using Templex

Learn how to run a simple DOE study on a cantilever beam to examine the influence of the length, width, and height of the beam on its volume, maximum bending stress, and deflection.

Before you begin, copy the model files used in this tutorial from <hst.zip>/HS-2005/ to your working directory.
You will create a Full factorial DOE to identify all of the main effects and all of the interactions between the beam's dimensions. The base input Templex template, beam.tpl, defines three input variables (L, B, and H) for the beam dimensions labeled as length, width, and height, respectively.


Figure 1. Cantilever Beam
{parameter(L,"Length",50,50,100)}
{parameter(B,"Width",2.5,2.5,5)}
{parameter(H,"Height",5,5,10)}
{P = 100}
{E = 2e11}
{M = P*L}
{c = H/2}
{I = (B*H^3)/12}
{MAX_STRESS = (M*c)/I}
{MAX_DISP = (P*L^3)/(3*E*I)}
{VOLUME = B*H*L}
{MAX_STRESS}
{MAX_DISP}
{VOLUME}

Perform the Study Setup

In this step you will add a study and load the input file into HyperStudy.

The input variables for the DOE study (length, width, and height) are selected as factors. A nominal run is performed (with Templex as the solver), and the output responses for the DOE study are selected (in this case: volume, max. stress, and max. displacement).

  1. Start HyperStudy.
  2. Start a new study in the following ways:
    • From the menu bar, click File > New.
    • On the ribbon, click .
  3. In the Add Study dialog, enter a study name, select a location for the study, and click OK.
  4. Go to the Define Models step.
  5. Add a Parameterized File model.
    1. From the Directory, drag-and-drop the beam.tpl file into the work area.


      Figure 2.
    2. In the Solver input file column, enter beam.tpl.
      This is the name of the solver input file HyperStudy writes during any evaluation.
    3. In the Solver execution script column, select Templex (templex).
  6. Click Import Variables.
    Three input variables are imported from the beam.tpl resource file.
  7. Go to the Define Input Variables step.
  8. Review the input variable's lower and upper bound ranges.

Perform Nominal Run

  1. Go to the Test Models step.
  2. Click Run Definition.
    An approaches/setup_1-def/ directory is created inside the study Directory. The approaches/setup_1-def/run__00001/m_1 directory contains the input file, which is the result of the nominal run.

Create and Evaluate Output Responses

In this step you will create three output responses: Max_Stress, Max_Disp, and Volume.

  1. Go to the Define Output Responses step.
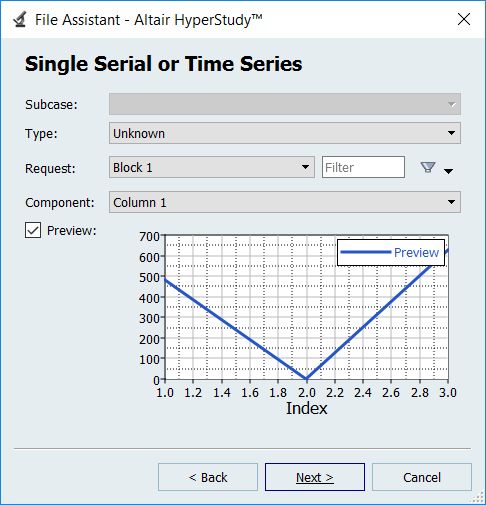
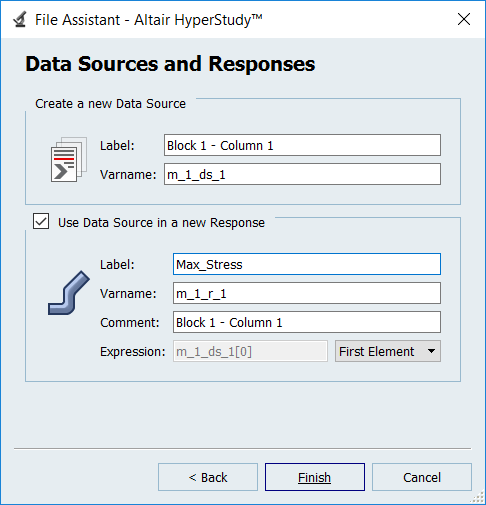
  2. Create the Max_Stress output response.
    1. From the Directory, drag-and-drop the beam.tpl file, located in approaches/setup_1-def/run__00001/m_1, into the work area.
    2. In the File Assistant dialog, set the Reading technology to Altair® HyperWorks® and click Next.
    3. Select Single item in a time series, then click Next.
    4. Define the following options, then click Next.
      • Set Type to Unknown.
      • Set Request to Block 1.
      • Set Component to Column 1.


      Figure 3.
    5. Label the output response Max_Stress.
    6. Set Expression to First Element.
      Note: Because there is only a single value in this data source, HyperStudy inserts [0] after m_1_ds_1, thereby choosing the first (and only) entry in the data source.
    7. Click Finish.


      Figure 4.
  3. Repeat step 2 to create the Max_Disp and Volume output responses.
  4. In the work area, Expression field, edit expressions.
    1. For Max_Disp, after m_1_ds_2, change [0] to [1].
    2. For Volume, after m_1_ds_3, change [0] to [2].


    Figure 5.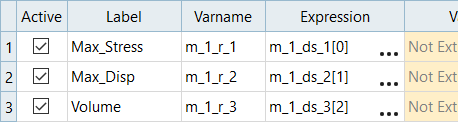
  5. Click Evaluate to extract the response values.

Run DOE

In this step you will set up a DOE approach through the selection of a DOE matrix and input variables.

Input variables can either be controlled or uncontrolled. In this exercise, a full factorial DOE matrix is considered. This provides the main effect of the input variables and their interactions with one another for selected output responses. The length, width, and depth of the input variables are introduced as controlled and their effects are studied for the following output responses: maximum stress, maximum displacement, and volume.

  1. Add a DOE.
    1. In the Explorer, right-click and select Add from the context menu.
      The Add dialog opens.
    2. For Definition from, select an approach.
    3. Select DOE and click OK.
  2. Go to the DOE 1 > Specifications step.
  3. In the work area, set the Mode to Full Factorial.
  4. Click Apply.
  5. Go to the DOE 1 > Evaluate step.
  6. Click Evaluate Tasks.
  7. Monitor the progress of the evaluation by clicking the Evaluation Data and Evaluation Plot tabs.
  8. Go to the DOE 1 > Post-Processing step.
  9. Review the main effect of each controlled parameter on a selected output response.
    1. Click the Linear Effects tab.
    2. Above the Channel selector, click to plot the linear effects.
    3. Use the Channel selector to select the all input variables and the Max_Stress output response.
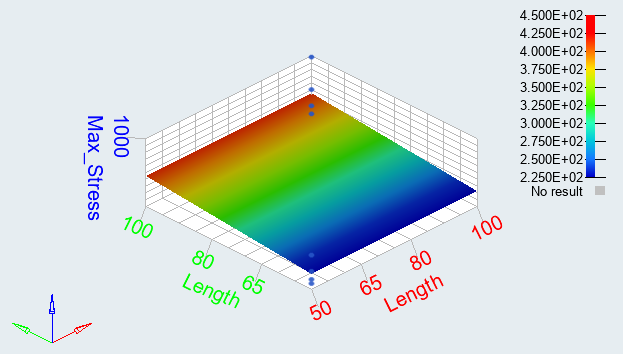
    Review the effects of a single input variable on an output response, or multiple input variables on an output response.


    Figure 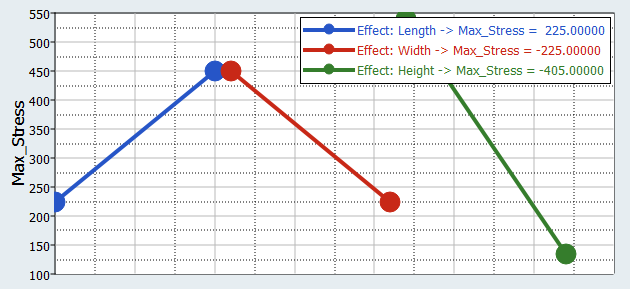6.
    As illustrated in Figure 6, as the length increases from 50 to 100 units, the max stress increases from 225 to 450. Increasing the width from 2.5 to 5 units decreases the max stress by the same amount. The contributions for max stress from both length and width are identical. Increasing the height from 5 to 10 units decreases the max stress by a larger extent (from 530 to 130). It is clear that for the max stress output response, height has a larger main effect than length or width.
    Input Variable Max_Stress - Lower Bound Max_Stress - Upper Bound
    Length 225 450
    Width 450 225
    Height 540 135
  10. Click the Distribution tab to review a histogram of Max Stress.


    Figure 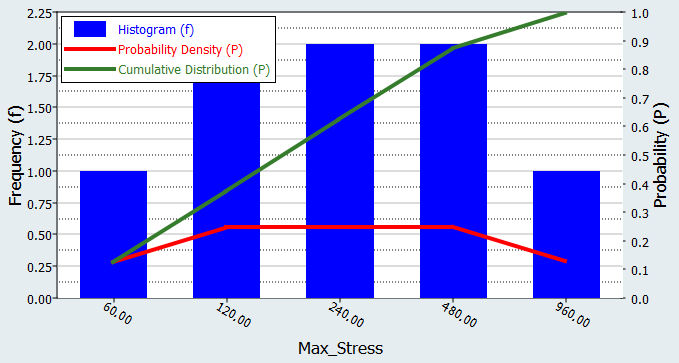7.

Run Fit for Regression Equation

In this step you will create approximations for the DOE study.

A first order regression equation for each output response (Max Stress, Max disp, and Volume) is created based on the DOE study. Since the input variables are of two levels, only the first order equation can be generated.

  1. Add a Fit.
    1. In the Explorer, right-click and select Add from the context menu.
    2. In the Add dialog, select Fit and click OK.
  2. Import matrix.
    1. Go to the Fit 1 > Select Matrices step.
    2. Click Add Matrix.
    3. In the work area, set Matrix Source to DOE 1 (doe_1).
    4. Click Import Matrix.


    Figure 8.
  3. Define specifications.
    1. Go to the Fit 1 > Specifications step.
    2. In the work area, Fit Type column, select Least Squares Regression (LSR) for all output responses.
    3. Click Apply.


    Figure 9.
  4. Evaluate tasks.
    1. Go to the Fit 1 > Evaluate step.
    2. Click Evaluate Tasks.
  5. Go to the Fit 1 > Post-Processing step.
  6. Click the Residuals tab.
    The Residuals table displays the difference between the output response value from the solver and the output response value calculated from the regression equation. This table can also be used to determine which runs are generating more errors in the regression model. The % error column shows that the predicted output response is not close to the observed value. The % error can be reduced if more levels are chosen for example, using a three-level design in this exercise.


    Figure 10.
  7. Plot output responses vs. input variables.
    1. Click the Trade-Off tab.
    2. In the Inputs pane, select the X Axis and Y Axis checkboxes for Length.
    3. Using the Channel selector, selector Max_Stress.
    4. Review the plot in the Outputs pane.


    Figure 11.