HS-2201: Use Existing Design Data from an Excel Spreadsheet with a Lookup Model

Learn how to perform an optimization study for an application where only design data in a .csv file is available (that is no simulation model exists).

Before you begin, copy the model files used in this tutorial from <hst.zip>/HS-2201/ to your working directory.

The objective of this tutorial is to create a fit (approximation) using the designs in the study_data.csv file and then to perform an optimization study using the fit.

The first and second columns contain the values of the two input variables for each design, and the third and fourth columns contain the results of a DOE study previously run. Sixteen designs have been evaluated.

Perform the Study Setup

  1. Start HyperStudy.
  2. Start a new study in the following ways:
    • From the menu bar, click File > New.
    • On the ribbon, click .
  3. In the Add Study dialog, enter a study name, select a location for the study, and click OK.
  4. Go to the Define Models step.
  5. Add a Lookup model.
    1. Click Add Model.
    2. In the Add dialog, select Lookup and click OK.
    3. In the work area, Resource column, click .
    4. In the HyperStudy – Load model resource dialog, navigate to your working directory and open the study_data.csv file.
  6. Import variables.
    1. Click Import Variables.
    2. In the Import Variables dialog, Number of design variables field, enter 2.
    3. Click OK.
    Figure 1.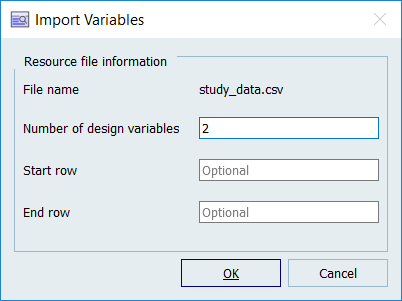


  7. Go to the Define Input Variables step.
  8. Review the two input variables that were imported from the study_data.csv file.
    Figure 2.


Perform Nominal Run

  1. Go to the Test Models step.
  2. Click Run Definition.
    An approaches/setup_1-def/ directory is created inside the study Directory. The approaches/setup_1-def/run__00001/m_1 directory contains the input file, which is the result of the nominal run.

Review Output Responses

  1. Go to the Define Output Responses step.
  2. Review the two output responses that were imported from the study.csv file.
    Figure 3.


Import DOE Results from CSV

  1. Add a DOE.
    1. In the Explorer, right-click and select Add from the context menu.
      The Add dialog opens.
    2. From Select Type, choose DOE.
    3. For Definition from, select an approach.
    4. Select Setup and click OK.
  2. Go to the DOE 1 > Specifications step.
  3. In the work area, set the Mode to Run Matrix.
  4. From the Settings tab, Matrix File field, click .
  5. In the Open dialog, navigate to your working directory and open the study_data.csv file.
    Figure 4.


  6. Click Apply.
  7. Go to the DOE 1 > Evaluate step.
  8. Click Evaluate Tasks.

Run Fit

  1. Add a Fit.
    1. In the Explorer, right-click and select Add from the context menu.
    2. In the Add dialog, select Fit Existing Data and Setup, and click OK.
  2. Import matrix.
    1. Go to the Fit 1 > Select Matrices step.
    2. Click Add Matrix.
    3. Click Import Matrix.
  3. Define specifications.
    1. Go to the Fit 1 > Specifications step.
    2. Leave the Fit Type set to FAST (Fit Automatically Selected by Training ) for each output response.
      Note: By default, FAST automatically selects the best Fit type from all available Fits. You can manually select the Fit types FAST can choose by highlighting one or more responses in the work area and selecting Fits from the Settings tab.
    3. Click Apply.
    Figure 5.


  4. Evaluate tasks.
    1. Go to the Fit 1 > Evaluate step.
    2. Click Evaluate Tasks.
  5. Go to the Fit 1 > Post-Processing step.
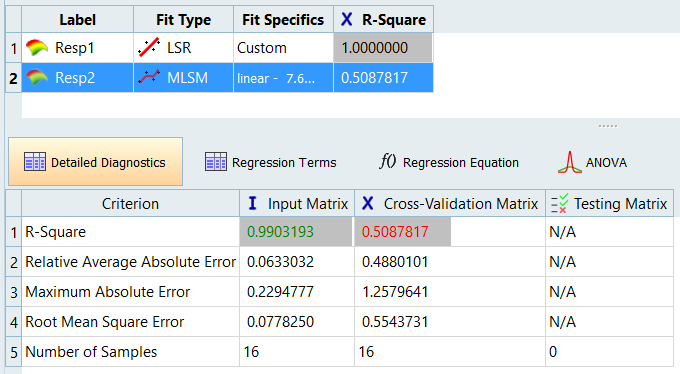
  6. Click the Diagnostics tab.
    Resp1 has the best Fit using LSR with custom terms; the Regression Terms tab shows that only linear terms are required. Resp2 has the best results using a MLSM. For Resp2, the R-square value that is based on the Input Matrix shows that the model accuracy is very good. The moderate value for the cross validation indicates that the model may benefit from more data because its accuracy is quite dependent on the complete set of point. Removing any points from the input set can significantly alter the Fit’s predictions.
    Figure 6.