HS-2200: Use Existing Design Data from an Excel Spreadsheet

In this tutorial, you will learn how to build a predictive model (Fit) for an application where only design data in a Microsoft Excel spreadsheet is available (that is, no simulation model exists).

Before you begin, copy the model files used in this tutorial from <hst.zip>/HS-2200/ to your working directory.

The objective of this tutorial is to create a Fit (approximation) using the designs in the spreadsheet.

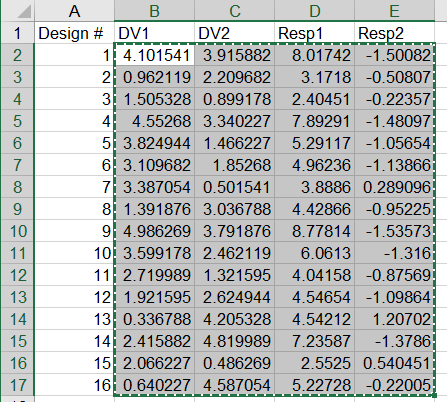
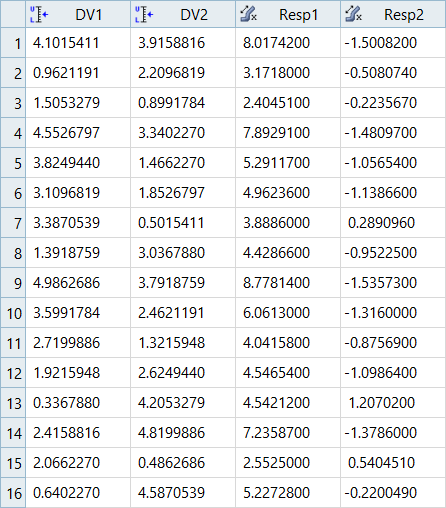
The spreadsheet used here contains five columns. The first column contains the numbering of the designs, the second and third columns contain the values of the two input variables for each design, and the fourth and the fifth columns contain the results of a DOE study previously run. Sixteen designs have been evaluated.

Perform the Study Setup

  1. Start HyperStudy.
  2. Start a new study in the following ways:
    • From the menu bar, click File > New.
    • On the ribbon, click .
  3. In the Add Study dialog, enter a study name, select a location for the study, and click OK.
  4. Go to the Define Models step.
  5. Add an Internal Math model.
    1. Click Add Model.
    2. In the Add dialog, add one Internal Math model.
  6. Go to the Define Input Variables step.
  7. Add input variables.
    1. Click Add Input Variable twice.
    2. Optional: Copy the input variable labels from the study.xls spreadsheet, and paste them into the Labels column of the work area.
      Note: When you paste the input variable labels into the work area, select Paste transpose from the context menu.
      Figure 1.


Perform Nominal Run

  1. Go to the Test Models step.
  2. Click Run Definition.
    An approaches/setup_1-def/ directory is created inside the study Directory. The approaches/setup_1-def/run__00001/m_1 directory contains the input file, which is the result of the nominal run.

Create and Evaluate Output Responses

  1. Go to the Define Output Responses step.
  2. Click Add Output Response twice.
  3. Optional: Copy the output response labels from the study.xls spreadsheet, and paste them into the Label column in the work area.
    Note: When you paste the input variable labels into the work area, select Paste transpose from the context menu.
    Figure 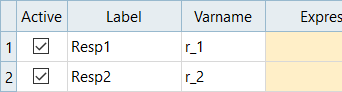2.


Run DOE

  1. Add a DOE.
    1. In the Explorer, right-click and select Add from the context menu.
      The Add dialog opens.
    2. From Select Type, choose DOE.
    3. For Definition from, select an approach.
    4. Select Setup and click OK.
  2. Go to the DOE 1 > Specifications step.
  3. In the work area, set the Mode to None.
  4. Click Apply.
  5. Edit run matrix.
    1. In the top, right of the work area, select Edit > Run Matrix.
      Figure 3.


    2. In the Edit Run Matrix dialog, click Add Run to add 16 runs to the matrix, as there are 16 runs in the study.xls spreadsheet.
    3. Open the study.xls spreadsheet in Excel.
    4. Copy all of the input variable and output response data for each run in the spreadsheet.
      Figure 4.


    5. In the Edit Run Matrix dialog, highlight all of the runs in the matrix.
    6. Right-click on the highlighted runs, and select Paste from the context menu.
      HyperStudy pastes the input variable and output response data that you copied from the study.xls spreadsheet into the run matrix.
      Figure 5.


    7. Click Apply.
    8. Click OK.

Run Fit

  1. Add a Fit.
    1. In the Explorer, right-click and select Add from the context menu.
    2. In the Add dialog, select Fit Existing Data and Setup, and click OK.
  2. Import matrix.
    1. Go to the Fit 1 > Select Matrices step.
    2. Click Add Matrix.
    3. Click Import Matrix.
    Figure 6.


  3. Define specifications.
    1. Go to the Fit 1 > Specifications step.
    2. Leave the Fit Type set to FAST (Fit Automatically Selected by Training ).
    3. Click Apply.
  4. Evaluate tasks.
    1. Go to the Fit 1 > Evaluate step.
    2. Click Evaluate Tasks.
  5. Go to the Fit 1 > Post-Processing step.
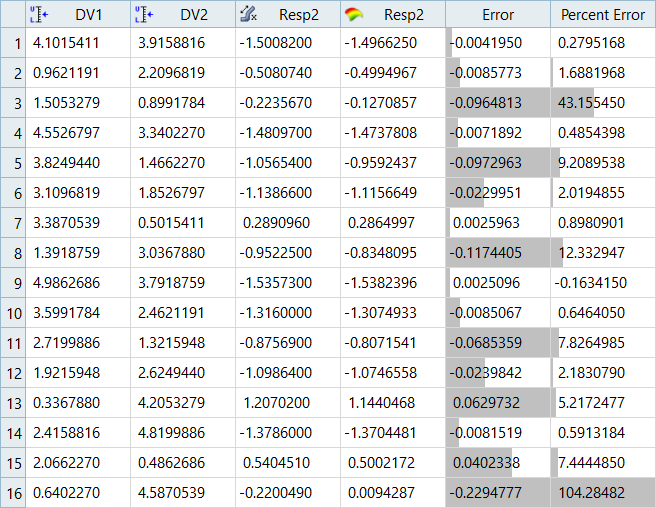
  6. Click the Residuals tab to investigate the accuracy of your approximation. From the table you can see that this approximation is not as good.
    Figure 7.