VISCOSITY_MODEL
Specifies a viscosity model for the flow equation.
Type
AcuSolve Command
Syntax
VISCOSITY_MODEL("name") {parameters...}
Qualifier
User-given name.
Parameters
- type (enumerated) [=none]
- Type of the viscosity.
- constant or const
- Constant viscosity. Requires viscosity.
- ramped or ramp
- Ramp the viscosity to a constant value. Requires viscosity.
- power_law
- Non-Newtonian power law viscosity model. Requires power_law_viscosity, power_law_time_constant, power_law_index and power_law_lower_strain_rate.
- bingham
- Non-Newtonian Bingham viscosity model. Requires bingham_viscosity, bingham_yield_stress, bingham_stress_growth_exponent, bingham_time_constant, bingham_index and bingham_infinite_shear_viscosity.
- carreau
- Non-Newtonian Carreau-Yasuda viscosity model. Requires carreau_zero_shear_viscosity, carreau_infinite_shear_viscosity, carreau_time_constant, carreau_index and carreau_transition_index.
- gas_kinetic
- Gas kinetic viscosity model for gases only. Requires GAS_KINETIC_MODEL.
- sutherland
- Sutherland temperature dependent viscosity model. Requires sutherland_reference_viscosity, sutherland_reference_temperature, sutherland_constant.
- piecewise_linear or linear
- Piecewise linear curve fit. Requires curve_fit_values and curve_fit_variable.
- cubic_spline or spline
- Cubic spline curve fit. Requires curve_fit_values and curve_fit_variable.
- user_function or user
- User-defined function. Requires user_function, user_values and user_strings.
- viscosity or visc (real) >=0 [=0]
- Constant value of the dynamic viscosity. Used with constant and ramped types.
- power_law_viscosity (real) >=0 [=0]
- Power law model reference viscosity. Used with power_law type.
- power_law_time_constant (real) >=0 [=0]
- Power law model time constant. Used with power_law type.
- power_law_index (real) [=1]
- Power law model power index. Used with power_law type.
- power_law_lower_strain_rate (real) >=0 [=0]
- Power law model lower limit of strain rate. Used with power_law type.
- bingham_viscosity (real) >0 [=1]
- Bingham model reference viscosity. Used with bingham type.
- bingham_yield_stress (real) >=0 [=0]
- Bingham model yield stress. Used with bingham type.
- bingham_stress_growth_exponent (real) >0 [=500]
- Bingham model unyielded stress region growth rate exponent. Used with bingham type.
- bingham_time_constant (real) >0 [=1]
- Bingham model power law time constant. Used with bingham type.
- bingham_index (real) [=1]
- Bingham model power law index. Used with bingham type.
- bingham_infinite_shear_viscosity (real) [=0]
- Bingham model minimum viscosity. Used with bingham type.
- carreau_zero_shear_viscosity (real) >=0 [=0]
- Carreau model viscosity at zero shear rate. Used with carreau type.
- carreau_infinite_shear_viscosity (real) >=0 [=0]
- Carreau model viscosity at infinite shear rate. Used with carreau type.
- carreau_time_constant (real) >=0 [=0]
- Carreau model power law time constant. Used with carreau type.
- carreau_index (real) [=1]
- Carreau model power law index. Used with carreau type.
- carreau_transition_index (real) >0 [=2]
- Carreau model transition index. Used with carreau type.
- carreau_temperature_dependence_type (enumerated) [=none]
- Types to add the temperature dependence terms to the Carreau Yasuda viscosity material
to account for shear heating due to viscous dissipation. Used with
carreau type when temperature =
advective_diffusive under the EQUATION command and
viscous_heating = on in
ELEMENT_SET.
- Arrhenius
- Arrhenius model. Requires activation energy.
- William_Landel_Ferry
- William Landel Ferry (WLF) model. Requires William_Landel_Ferry_coefficient_C1, William_Landel_Ferry_coefficient_C2, glass_transition_temperature.
- exponential
- Exponential model. Requires exponential_reference_temperature and exponential_beta_coefficient.
- activation_energy (real) >0 [=16628]
- Arrhenius model constant to define the temperature sensitivity. Used with carreau type and carreau_temperature_dependence_type = Arrhenius.
- William_Landel_Ferry_coefficient_C1 (real) > 0 [=17.44]
- William-Landel-Ferry (WLF) model constant. Used with carreau type and carreau_temperature_dependence_type = William_Landel_Ferry.
- William_Landel_Ferry_coefficient_C2 (real) > 0 [=51.6]
- William-Landel-Ferry (WLF) model constant. Used with carreau type and carreau_temperature_dependence_type = William_Landel_Ferry.
- glass_transition_temperature (real) > 0 [=320]
- Glass transition temperature used in the William-Landel-Ferry (WLF) model. Used with carreau type and carreau_temperature_dependence_type = William_Landel_Ferry.
- exponential_reference_temperature (real) > 0 [=350]
- Reference temperature defined in the exponential model. Used with carreau type and carreau_temperature_dependence_type = exponential.
- exponential_beta_coefficient (real) > 0 [=0.005]
- Exponential model constant. Used with carreau type and carreau_temperature_dependence_type = exponential.
- sutherland_reference_viscosity (real) > = 0 [=0.01716]
- Sutherland model reference viscosity at sutherland_reference_temperature. Used with sutherland type.
- sutherland_reference_temperature (real) > 0 [=273]
- Sutherland model reference temperature corresponding to sutherland_reference_viscosity. Used with sutherland type.
- sutherland_constant (real) > 0 [=111]
- Sutherland model constant. Used with sutherland type.
- curve_fit_values or curve_values array [={0,0}]
- A two-column array of independent-variable/viscosity data values. Used with piecewise_linear and cubic_spline types.
- curve_fit_variable or curve_var (enumerated) [=temperature]
- Independent variable of the curve fit. Used with piecewise_linear
and cubic_spline types.
- x_coordinate or xcrd
- X-component of coordinates.
- y_coordinate or ycrd
- Y-component of coordinates.
- z_coordinate or zcrd
- Z-component of coordinates.
- x_reference_coordinate or xrefcrd
- X-component of reference coordinates.
- y_reference_coordinate or yrefcrd
- Y-component of reference coordinates.
- z_reference_coordinate or zrefcrd
- Z-component of reference coordinates.
- pressure or pres
- Pressure.
- temperature or temp
- Temperature.
- species_1 or spec1
- Species 1.
- species_2 or spec2
- Species 2.
- species_3 or spec3
- Species 3.
- species_4 or spec4
- Species 4.
- species_5 or spec5
- Species 5.
- species_6 or spec6
- Species 6.
- species_7 or spec7
- Species 7.
- species_8 or spec8
- Species 8.
- species_9 or spec9
- Species 9.
- strain_rate_second_invariant or strain_i2
- Second invariant of the strain rate tensor.
- user_function or user (string) [no default]
- Name of the user-defined function. Used with user_function type.
- user_values (array) [={}]
- Array of values to be passed to the user-defined function. Used with user_function type.
- user_strings (list) [={}]
- Array of strings to be passed to the user-defined function. Used with user_function type.
- multiplier_function (string) [=none]
- User-given name of the multiplier function for scaling the viscosity. If none, no scaling is performed.
Description
This command specifies a dynamic viscosity model for the flow (momentum) equation. This model is only applicable to fluid element sets.
VISCOSITY_MODEL( "my viscosity model" ) {
type = constant
viscosity = 1.781e-5
}
MATERIAL_MODEL( "my material model" ) {
viscosity_model = "my viscosity model"
...
}
ELEMENT_SET( "fluid elements" ) {
material_model = "my material model"
medium = fluid
...
}The viscous stress tensor  is given
by:
is given
by:
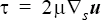
where is the dynamic viscosity and is the symmetric part of the strain-rate tensor.
A constant type applies a spatially constant viscosity model, as in the above example. This is the simplest case of a Newtonian model for the stress tensor.
The power_law type defines a non-Newtonian viscosity model in which the dynamic-viscosity is a function of the velocity field:
where is the reference viscosity, given by power_law_viscosity; is the time constant, given by power_law_time_constant; n is the power index, given by power_law_index; Smin is the lower limit of the strain rate, given by power_law_lower_strain_rate; and I2 is the second invariant of the strain rate tensor:
One of the commonly used models for characterizing non-Newtonian viscosity fluids is the power law model. This model describes the behavior of shear thinning fluids, where the viscosity decreases as the shear rate increases. The relationship between the viscosity and the shear rate can be expressed as follows:
where represents the viscosity (Pa sec), is the shear rate (1/sec), n is the power law index; is the flow consistency.
For example, if the viscometer measurement yields the following curve-fit result
The power index ( ) can be obtained from . The power law viscosity can be calculated by substituting 200 to the equation 2 as shown below. It is important to account for a factor of 2 due to definition of the second invariant of the strain tensor:
Thus, power law viscosity is .
VISCOSITY_MODEL( "Basic Power Law" ) {
type = power_law
power_law_viscosity = 287.8
power_law_time_constant = 1.0
power_law_index = -0.05
power_law_lower_strain_rate = 0.1
}The bingham type defines another non-Newtonian viscosity model in which Papanastasiou's unyielded stress region and power law modifications are added to the basic Bingham viscosity model:
where is the reference viscosity, given by bingham_viscosity; is the time constant, given by bingham_time_constant; n is the power index, given by bingham_index; is the yield stress, given by bingham_yield_stress; M is the unyielded stress region growth rate exponent, given by bingham_stress_growth_exponent; ∞ is the viscosity at infinite shear rate (or equivalently the minimum viscosity), given by bingham_infinite_shear_viscosity; and g is the square root of the second invariant of the strain rate tensor:
VISCOSITY_MODEL( "Basic Bingham Law" ) {
type = bingham
bingham_viscosity = 0.001
bingham_yield_stress = 10
}VISCOSITY_MODEL( "Bingham Law with Papanastasiou exponent" ) {
type = bingham
bingham_viscosity = 0.001
bingham_yield_stress = 10
bingham_stress_growth_exponent = 1000
}VISCOSITY_MODEL( "Bingham Law with Papanastasiou exponent and power law" ) {
type = bingham
bingham_viscosity = 0.001
bingham_yield_stress = 10
bingham_stress_growth_exponent = 1000
bingham_time_constant = 1
bingham_index = 0.75
}The carreau type defines a third non-Newtonian viscosity model:
where 0 is the viscosity at zero shear rate, given by carreau_zero_shear_viscosity; ∞ is the viscosity at infinite shear rate, given by carreau_infinite_shear_viscosity; is the time constant, given by carreau_time_constant; n is the power index, given by carreau_index; a is the transition index, given by carreau_transition_index; and g is the square root of the second invariant of the strain rate tensor (see above). In this form this model is known as the Carreau-Yasuda model. If a = 2, then the classic Carreau model is recovered.
VISCOSITY_MODEL( "Carreau Model" ) {
type = carreau
carreau_zero_shear_viscosity = 681.8
carreau_infinite_shear_viscosity = 0.17
carreau_time_constant = 31.7
carreau_index = 0.11
carreau_transition_index = 2
}The sutherland type defines a temperature dependent viscosity model according to the following equation:
where is the sutherland_reference_viscosity at the specified sutherland_reference_temperature ( ), is the model temperature and is the sutherland_constant.
VISCOSITY_MODEL( "Sutherland Model" ) {
type = sutherland
sutherland_reference_viscosity = 1.716e-5
sutherland_reference_temperature = 273.0
sutherland_constant = 111
}VISCOSITY_MODEL( "ramped viscosity model" ) {
type = ramped
viscosity = 1.781e-5
}starts with a viscosity of 1.781 x 10-2 at time step one and reduces the viscosity until time step 10, at which time a viscosity of 1.781 x 10-5 is used.
VISCOSITY_MODEL( "curve fit viscosity model" ) {
type = piecewise_linear
curve_fit_values = { 273, 1.72e-5 ;
323, 1.95e-5 ;
373, 2.17e-5 ;
423, 2.38e-5 ; }
curve_fit_variable = temperature
}defines viscosity as a function of temperature. In this case, the problem must contain a temperature equation; see the EQUATION command. The curve_fit_values parameter is a two-column array corresponding to the independent variable and the viscosity values. The independent variable values must be in ascending order. The limit point values of the curve fit are used when curve_fit_variable falls outside of the curve fit limits.
273 1.72e-5
323 1.95e-5
373 2.17e-5
423 2.38e-5VISCOSITY_MODEL( "curve fit viscosity model" ) {
type = piecewise_linear
curve_fit_values = Read( "viscosity.fit" )
curve_fit_variable = temperature
}A viscosity of type user_function may be used to model more complex behaviors; the see AcuSolve User-Defined Functions Manual for a detailed description of user-defined functions.
VISCOSITY_MODEL( "UDF viscosity model" ) {
type = user_function
user_function = "usrViscosityExample"
user_values = { 9000, # reference viscosity
12.5, # time constant
0.48 } # power index
}#include "acusim.h"
#include "udf.h"
UDF_PROTOTYPE( usrViscosityExample ) ; /* function prototype */
Void usrViscosityExample (
UdfHd udfHd, /* Opaque handle for accessing data */
Real* outVec, /* Output vector */
Integer nItems, /* Number of elements */
Integer vecDim /* = 1 */
) {
Integer elem ; /* an element counter */
Real exp ; /* exponent ( (index-1)/2 ) */
Real index ; /* power index */
Real invar2 ; /* second invariant of strain rate */
Real tConst ; /* time constant */
Real tConst2 ; /* scaling factor (tConst ^ 2) */
Real visc0 ; /* reference viscosity */
Real* gradV ; /* gradient of velocity */
Real* u11 ; /* partial u1 / partial x1 */
Real* u12 ; /* partial u1 / partial x2 */
Real* u13 ; /* partial u1 / partial x3 */
Real* u21 ; /* partial u2 / partial x1 */
Real* u22 ; /* partial u2 / partial x2 */
Real* u23 ; /* partial u2 / partial x3 */
Real* u31 ; /* partial u3 / partial x1 */
Real* u32 ; /* partial u3 / partial x2 */
Real* u33 ; /* partial u3 / partial x3 */
Real* usrVals ; /* user values */
udfCheckNumUsrVals( udfHd, 3 ) ; /* check for error */
usrVals = udfGetUsrVals( udfHd ) ; /* get the user vals */
visc0 = usrVals[0] ; /* reference visc. */
tConst = usrVals[1] ; /* time constant */
index = usrVals[2] ; /* index */
tConst2 = tConst * tConst ; /* for efficiency */
exp = (index - 1) / 2 ; /* for efficiency */
gradV = udfGetElmData( udfHd, UDF_ELM_GRAD_VELOCITY ) ; /* get the grad-vel. */
u11 = &gradV[0*nItems] ; /* localize u11 */
u12 = &gradV[1*nItems] ; /* localize u12 */
u13 = &gradV[2*nItems] ; /* localize u13 */
u21 = &gradV[3*nItems] ; /* localize u21 */
u22 = &gradV[4*nItems] ; /* localize u22 */
u23 = &gradV[5*nItems] ; /* localize u23 */
u31 = &gradV[6*nItems] ; /* localize u31 */
u32 = &gradV[7*nItems] ; /* localize u32 */
u33 = &gradV[8*nItems] ; /* localize u33 */
for ( elem = 0 ; elem < nItems ; elem++ ) {
invar2 = 2.
* ( u11[elem] * u11[elem]
+ u22[elem] * u22[elem]
+ u33[elem] * u33[elem]
+ (u12[elem]+u21[elem]) * (u12[elem]+u21[elem])
+ (u23[elem]+u32[elem]) * (u23[elem]+u32[elem])
+ (u31[elem]+u13[elem]) * (u31[elem]+u13[elem]) ;
outVec[elem] = visc0 ;
if ( tConst2 * invar2 > ) {
outVec[elem] = visc0 * pow( tConst2 * invar2, exp ) ;
}
}
} /* end of usrViscosityExample() */The dimension of the returned viscosity vector, outVec, is the number of elements.
VISCOSITY_MODEL( "similar to ramped viscosity model" ) {
type = constant
viscosity = 1.781e-5
multiplier_function = "ramped"
}
MULTIPLIER_FUNCTION( "ramped" ) {
type = piecewise_log_linear
curve_fit_values = { 1, 1000 ; 10, 1 }
curve_fit_variable = time_step
}In areas of turbulent flow the molecular viscosity is replaced by the total viscosity + t in the definition of the viscous stress tensor. The turbulent viscosity t is given by the turbulence model in use; see the EQUATION command for details.