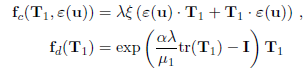VISCOELASTIC_MODEL

Type

AcuSolve Command

Syntax

VISCOELASTIC_MODEL("name") {parameters...}

Qualifier

User-given name.

Parameters

type (enumerated) [=none]

Type of the viscoelastic model.

none

No viscoelastic model.

oldroyd_b

Oldroyd-B model describing the viscoelastic behavior of fluid. Requires time_constant and viscosity_model.

giesekus

Giesekus model describing the viscoelastic behavior of fluid. Requires time_constant, giesekus_mobility_factor and viscosity_model.

phan_thien_tanner or ptt

Requires time_constant, phan_thien_tanner_extensibility_factor, phan_thien_tanner_differential_ratio, and viscosity_model.

user_function_viscoelastic

User-defined function. Requires user_function, user_values and user_strings.

viscosity_model (string) [none]

Refers to viscosity of the polymer. Valid models are described in the VISCOSITY_MODEL command. Used with oldroyd_b, giesekus, and phan_thien_tanner types.

time_constant (real) >=0 [=0]

Relaxation time. Used with oldroyd_b, giesekus, and phan_thien_tanner types.

time_constant _multiplier_function (string) [none]

Multiplier function used for scaling the time constant. Used with oldroyd_b, giesekus, and phan_thien_tanner types.

giesekus_mobility_factor or giesekus_alpha >=0 [=0]

Mobility factor that controls extensional viscosity and the ratio of second normal stress difference to the first normal stress. Shear thinning behavior is observed when the mobility factor is greater than zero. Used with giesekus model.

phan_thien_tanner_extensibility_factor or ptt_alpha (real) >=0 [=0]

Controls the level of shear thinning. Used with phan_thien_tanner model.

phan_thien_tanner_differential_ratio or ptt_xi (real) >=0 <=2 [=0]

Factor that controls extensional viscosity and accounts for the slip between the molecular network and the continuum medium. Used with phan_thien_tanner model.

user_function or user (string) [no default]

Name of the user-defined function. Used with user_function type.

user_values (array) [={}]

Array of values to be passed to the user-defined function. Used with user_function type.

user_strings (list) [={}]

Array of strings to be passed to the user-defined function. Used with user_function type.

multiplier_function (string) [=none]

User-given name of the multiplier function for scaling the viscosity. If none, no scaling is performed.

Description

This command specifies a viscoelastic model for the flow (momentum) equations. This model is only applicable to fluid element sets.

VISCOELASTIC_MODEL( "my viscoelastic model" ) {
   type             = oldroyd_b 
   time_constant    = 0.1
   viscosity_model  "polymer viscosity"
}
VISCOSITY_MODEL( "polymer viscosity" ) {
   type            = constant 
   viscosity       = 0.888888
}

In the case of viscoelastic fluids the stress depends on both instantaneous strain rate and strain history. For an Upper Convective Maxwell fluid, the constitutive equation is given by:

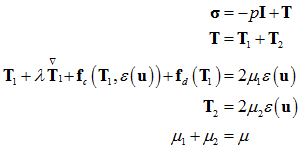
Here, $\sigma$ denotes the stress tensor, p is the fluid pressure, T represents the viscous stress tensor, $\lambda$ is the relaxation time, ${\mu }_1$ is the viscosity of the elastic polymer dissolved in a viscous solvent with viscosity ${\mu }_2$ . The coefficient f_c represents the rate at which the stress builds up and f_d represents the rate at which stress decays. $\stackrel{\nabla }{\text{T}}$ is the upper-convected derivative and $\dot{\epsilon }$ (u) is the rate-of-strain tensor:

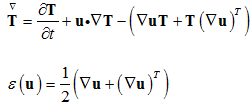
The solvent viscosity is defined by the parameter viscosity_model. For a complete description of viscosity models, refer to VISCOSITY_MODEL.

Oldroyd-B Model

The Oldroyd-B model can be obtained by defining:

Here you define only the relaxation time, given by time_constant and polymer viscosity, given by viscosity.

For example,

VISCOELASTIC_MODEL( "Oldroyd model" ) {
   type            = oldroyd_b
   time_constant   = 1.0
   viscosity_model = "Oldroyd model:viscoelastic"
}
VISCOSITY_MODEL( "Oldroyd model:viscoelastic" ) {
    type           = constant 
    viscosity      = 0.8888888888  # kg/m-sec
}

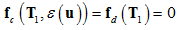
Giesekus Model

This model can be obtained by defining

Here you define the relaxation time, given by time_constant, polymer viscosity, given by viscosity, and the mobility factor $\alpha$ given by giesekus_mobility_factor or giesekus_alpha.

For example,

VISCOELASTIC_MODEL( "giesekus" ) {
   type             = giesekus
   viscosity_model  = "polymer viscosity"
   time_constant    = 0.1
   giesekus_alpha   = 0.1
}
VISCOSITY_MODEL( "polymer viscosity" ) {
   type             = constant 
   viscosity        = 0.888889
}

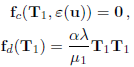
Phan-Thien-Tanner Model

This model can be obtained by defining:

Here you define the relaxation time, given by time_constant, polymer viscosity, given by viscosity, the extensibility factor, $\alpha$ , given by phan_thien_tanner_extensibility_factor or ptt_alpha, and diffential ratio $\varsigma$ given by phan_thien_tanner_differential_ratio or ptt_xi.

For example,

VISCOELASTIC_MODEL( "ptt" ) {
   type             = ptt 
   viscosity_model  = "polymer viscosity"
   time_constant    = 1.0
   ptt_alpha        = 0.25
   ptt_xi           = 0.1
}
VISCOSITY_MODEL( "polymer viscosity" ) {
   type            = constant 
   viscosity       = 0.888889
}