Turbulent Flow Through a Pipe

In this application, turbulent flow of air through a pipe is simulated. AcuSolve results are compared with experimental results as described in White (1991) and extracted from the Moody chart. The close agreement of AcuSolve results with experimental results validates the ability of AcuSolve to model turbulent flow within pipes.

Problem Description

The problem consists of air flowing through a pipe 0.004 m in diameter and 0.02 m long, as shown in the following image, which is not drawn to scale. The AcuSolve simulation utilizes periodic boundary conditions to obtain the fully developed profile within the pipe. The defined pressure drop, applied as a body force on the fluid volume, offsets the change in pressure due to the friction created by the no-slip walls of the pipe. The Reynolds number for this problem is approximately 8,250.
Figure 1. Critical Dimensions and Parameters for Simulating Turbulent Flow Through a Pipe


Figure 2. Mesh of a Periodic Segment Used for Simulating Turbulent Flow Through a Pipe


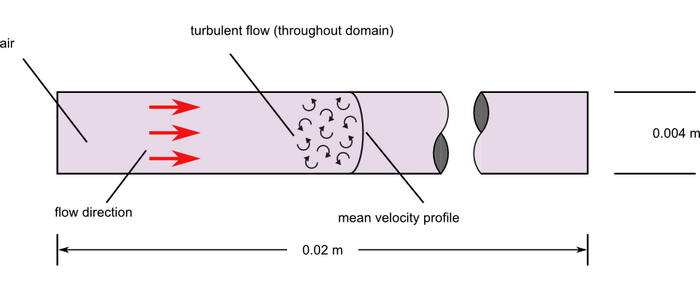
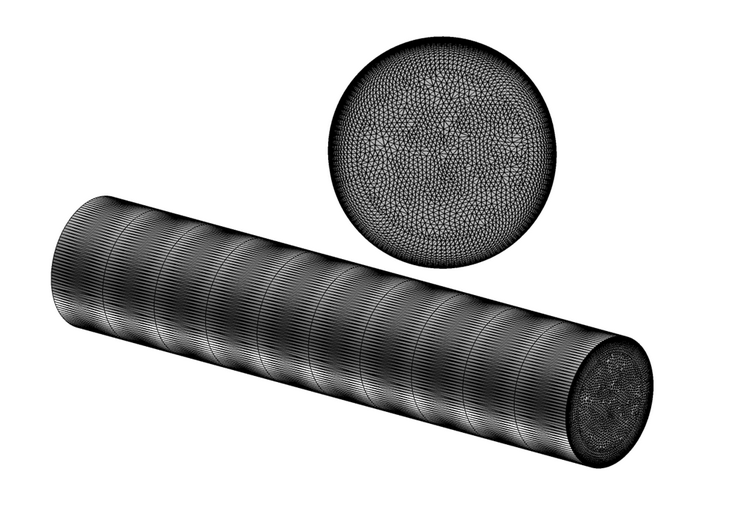
AcuSolve Results

The AcuSolve solution converged to a steady state and the results reflect the mean flow conditions with a turbulent velocity profile that is fully developed. The simulation was performed using the Spalart-Allmaras single-equation turbulence model. The velocity and eddy viscosity profiles are constant along the length of the pipe.
Figure 3. Velocity Contours for the Averaged Turbulent Flow


The experimental result for average velocity at the inlet is presented with the corresponding AcuSolve prediction in the following table.
Table 1.
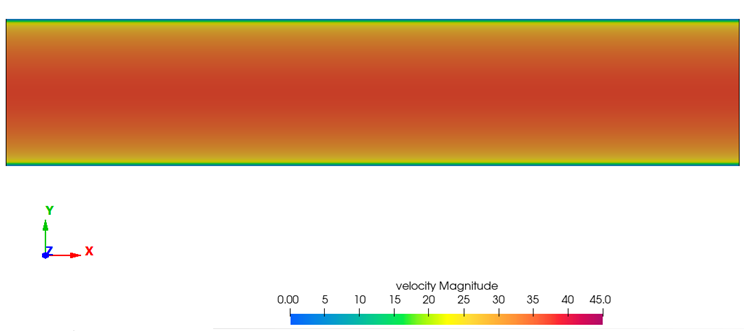
Experimental result AcuSolve prediction Percent deviation from experimental
Average inlet velocity 30.0 30.63 2.1

Summary

The AcuSolve solution compares well with the experimental result for average inlet velocity for turbulent flow through a pipe. In this application, the applied body force counteracts the change in pressure due to the viscous stresses near the pipe wall. The resulting friction factor for a smooth wall pipe and the specified Reynolds number is approximately 0.0326. With the imposed pressure drop defining the flow, the AcuSolve prediction of average inlet velocity is within 2.0 percent of the Darcy-Weisbach approximation.

Simulation Settings for Turbulent Flow Through a Pipe

SimLab database file: <your working directory >\pipe_turbulent\pipe_turbulent.slb.

Global

  • Problem Description
    • Flow - Steady State
    • Turbulence equation - Spalart Allmaras
  • Auto Solution Strategy
    • Relaxation factor - 0.4
  • Material Model
    • Air
      • Density - 1.225 kg/m3
      • Viscosity - 1.781e-05 kg/m-sec
  • Body Force
    • dpdx
      • Gravity
        • X-component - 3739.98 m/s2

    Model

  • Volumes
    • Fluid
      • Element Set
        • Material model - Air
        • Body force - dpdx
  • Surfaces
    • Inlet
      • Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
    • Outlet
      • Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
    • Wall
      • Simple Boundary Condition
        • Type - Wall
        • Roughness height - 0.0 mm
  • Periodics
    • Periodic 1
      • Periodic Boundary Condition
        • Type - Periodic

References

F. M. White. "Viscous Fluid Flow". Section 3-2.1. McGraw-Hill Book Co., Inc.. New York. 1991.

Experimental solution adapted from Darcy-Weisbach equation based on friction factor taken from the Moody chart with a Reynolds number of approximately 8,250.