TURBULENCE_WALL
Specifies a turbulent boundary layer wall.
Type
AcuSolve Command
Syntax
TURBULENCE_WALL("name") {parameters...}
Qualifier
User-given name.
Parameters
- shape (enumerated) [no default]
- Shape of the surfaces in this set.
- three_node_triangle or tri3
- Three-node triangle.
- four_node_quad or quad4
- Four-node quadrilateral.
- six_node_triangle or tri6
- Six-node triangle.
- element_set or elem_set (string) [no default]
- User-given name of the parent element set.
- surfaces (array) [no default]
- List of element surfaces.
- surface_sets (list) [={}]
- List of surface set names (strings) to use in this command. When using this option, the connectivity, shape, and parent element of the surfaces are provided by the surface set container and it is unnecessary to specify the shape, element_set and surfaces parameters directly to the TURBULENCE_WALL command. This option is used in place of directly specifying these parameters. In the event that both of the surface_sets and surfaces parameters are provided, the full collection of surface elements is read and a warning message is issued. The surface_sets option is the preferred method to specify the surface elements. This option provides support for mixed element topologies and simplifies pre-processing and post-processing.
- type (enumerated) [=low_reynolds_number]
- Type of the turbulence wall modeling.
- low_reynolds_number or low_re
- Low Reynolds number damping functions.
- wall_function or func
- Turbulence wall function.
- running_average_wall_function
- Turbulence wall function based on running average field.
- roughness_height (real) >=0 [=0]
- Average wall roughness height. Used with low_reynolds_number, wall_function, and running_average_wall_function type.
- wall_function_friction_factor >=1 [=1]
- Constant factor used to scale the turbulence friction within the first element off the wall. Used with turbulence_wall_type = wall_function and running_average_wall_function.
- wall_function_heat_flux_factor >=1 [=1]
- Constant factor used to scale the turbulent thermal conductivity within the first element off the wall. Used with type = wall_function and running_average_wall_function.
- active_type (enumerated) [=all]
- Type of the active flag. Determines which surfaces in this set will be active as turbulence
boundary layer walls.
- all
- All surfaces in this set are active.
- none
- No surface in this set is active.
- no_interface
- Only surfaces that are not in an interface surface set or do not find a contact surface of an appropriate medium are active.
Description
This command specifies the surfaces (element faces) bounding a turbulent boundary layer.
ELEMENT_SET( "interior" ) {
shape = four_node_tet
elements = { 1, 8, 3, 4, 9 ;
3, 3, 4, 9, 5 ;
... }
...
}
TURBULENCE_WALL( "no-slip wall" ) {
shape = three_node_triangle
element_set = "interior"
surfaces = { 1, 12, 9, 3, 4 ;
3, 52, 5, 3, 4 ; }
type = wall_function
roughness_height = 0.001
active_type = all
}specifies that two surfaces of the element set "interior" are on a no-slip boundary, that a turbulence wall function with an average wall roughness height of 0.001 is to be used to capture the turbulent boundary layer, and that both surfaces are active.
- Element Shape
- Surface Shape
- four_node_tet
- three_node_triangle
- five_node_pyramid
- three_node_triangle
- five_node_pyramid
- four_node_quad
- six_node_wedge
- three_node_triangle
- six_node_wedge
- four_node_quad
- eight_node_brick
- four_node_quad
- ten_node_tet
- six_node_triangle
The surfaces parameter contains the faces of the element set. This parameter is a multi-column array. The number of columns depends on the shape of the surface. For three_node_triangle, this parameter has five columns, corresponding to the element number (of the parent element set), a unique (within this set) surface number, and the three nodes of the element face. For four_node_quad, surfaces has six columns, corresponding to the element number, a surface number, and the four nodes of the element face. For six_node_triangle, surfaces has eight columns, corresponding to the element number, a surface number, and the six nodes of the element face. One row per surface must be given. The three, four, or six nodes of the surface may be in any arbitrary order, since they are reordered internally based on the parent element definition.
1 12 9 3 4
3 52 5 3 4TURBULENCE_WALL( "no-slip wall" ) {
shape = three_node_triangle
element_set = "interior"
surfaces = Read( "free.srf" )
...
}SURFACE_SET( "tri faces" ) {
surfaces = { 1, 1, 1, 2, 4 ;
2, 2, 3, 4, 6 ;
3, 3, 5, 6, 8 ; }
shape = three_node_triangle
volume_set = "tetrahedra"
}
SURFACE_SET( "quad faces" ) {
surfaces = { 1, 1, 1, 2, 4, 9 ;
2, 2, 3, 4, 6, 12 ;
3, 3, 5, 6, 8, 15 ; }
shape = four_node_quad
volume_set = "prisms"TURBULENCE_WALL ( "no-slip wall" ) {
surface_sets = {"tri_faces", "quad_faces"}
...
}tri faces
quad facesTURBULENCE_WALL ( "no-slip wall" ) {
surface_sets = Read("surface_sets.srfst")
...
}The mixed topology version of the TURBULENCE_WALL command is preferred. This version provides support for multiple element topologies within a single instance of the command and simplifies pre-processing and post-processing. In the event that both the surface_sets and surfaces parameters are provided in the same instance of the command, the full collection of surface elements is read and a warning message is issued. Although the single and mixed topology formats of the commands can be combined, it is strongly recommended that they are not.
A low_reynolds_number type specifies that the low Reynolds number damping
functions are to be used in modeling the boundary layer. This model integrates the
turbulence flow all the way to the boundary. As a result, this option is more
accurate, provided that sufficient mesh density is used. For the Spalart-Allmaras
turbulence model,  (defined
below) of the first mesh point must be less than 10 (preferably 5); otherwise, gross
errors in traction, heat flux, and mass transfer may result.
(defined
below) of the first mesh point must be less than 10 (preferably 5); otherwise, gross
errors in traction, heat flux, and mass transfer may result.
A wall_function type specifies that the turbulence "law of the wall" is to be
assumed near the wall. Turbulence wall functions allow for coarser meshes. For the
Spalart-Allmaras turbulence model, for example,  of the
first mesh point may be as large as 300. On the other hand, the law of the wall
applies only to simple turbulent boundary layers. The implemented wall function is
valid only for non-separated flows with mild pressure gradients.
of the
first mesh point may be as large as 300. On the other hand, the law of the wall
applies only to simple turbulent boundary layers. The implemented wall function is
valid only for non-separated flows with mild pressure gradients.
Unlike some wall function implementations there is no minimum  requirement in AcuSolve. For small values of
requirement in AcuSolve. For small values of  the two
types become equivalent. The velocity law of the wall is given by:
the two
types become equivalent. The velocity law of the wall is given by:

with a transition region for 5 < 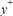 < 30 .
These two parts are referred to as the "viscous sublayer" and the "logarithmic
layer". The non dimensional distance to the wall
< 30 .
These two parts are referred to as the "viscous sublayer" and the "logarithmic
layer". The non dimensional distance to the wall  and
velocity
and
velocity  are defined by:
are defined by:

where  is the
kinematic viscosity,
is the
kinematic viscosity,  is the
turbulent friction velocity,
is the
turbulent friction velocity,  is the
wall shear, ρ is the density, U is the velocity
parallel to the wall, and y is the normal
distance to the wall. The logarithmic layer requires two experimentally determined
parameters:
is the
wall shear, ρ is the density, U is the velocity
parallel to the wall, and y is the normal
distance to the wall. The logarithmic layer requires two experimentally determined
parameters: 
The temperature law of the wall is similar:

plus a transition region. The non dimensional temperature is defined by

where, in addition to the velocity parameters, T is the
temperature,  is the
wall temperature,
is the
wall temperature,  is the
friction temperature,
is the
friction temperature,  is the
wall heat flux, and
is the
wall heat flux, and  is the
heat capacity. The molecular Prandtl number is
is the
heat capacity. The molecular Prandtl number is 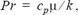 where μ
is the dynamic viscosity and k is the thermal
conductivity. The turbulent Prandtl number is modeled as a constant: the default is
where μ
is the dynamic viscosity and k is the thermal
conductivity. The turbulent Prandtl number is modeled as a constant: the default is
 but can be changed in CONDUCTIVITY_MODEL. The curve fit for the
intercept A is:
but can be changed in CONDUCTIVITY_MODEL. The curve fit for the
intercept A is:

The species law of the wall has the same form as for temperature:

plus a transition region. The nondimensional species is defined by

where, in addition to the parameters defined above, Φ is the species,  is the
wall species,
is the
wall species,  is the
friction species, and
is the
friction species, and  is the
wall species flux. The molecular Schmidt number is
is the
wall species flux. The molecular Schmidt number is  where
D is the species diffusivity. The turbulent
Schmidt number is modeled as a constant: the default is
Sct = 0.91, but can be changed in
DIFFUSIVITY_MODEL. The function
A is the same as for the temperature law of
the wall.
where
D is the species diffusivity. The turbulent
Schmidt number is modeled as a constant: the default is
Sct = 0.91, but can be changed in
DIFFUSIVITY_MODEL. The function
A is the same as for the temperature law of
the wall.
For simple attached turbulent boundary layers the required distance from the wall of the first
mesh point can be estimated given a desired  value.
The Reynolds number is
value.
The Reynolds number is

where x is the streamwise distance from the beginning of the
boundary layer and  is the
freestream velocity. An approximate correlation for the wall shear is given
by:
is the
freestream velocity. An approximate correlation for the wall shear is given
by:

From this the distance to the first node may be derived:

The extremely weak dependence on Reynolds number allows this procedure to work well with only a
rough estimate of the Reynolds number. For pipe flow a similar relationship valid
for  may be derived:
may be derived:

where 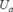 is the average pipe velocity and the Reynolds number
is the average pipe velocity and the Reynolds number  is based on
is based on 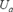 and the pipe diameter.
and the pipe diameter.
Normally, designing a mesh based on the turbulent velocity profile is sufficient to resolve the temperature and species boundary layers as well.
Specification of a turbulence wall via this command does not enforce a no-slip condition on the given surface. The no-slip velocity and proper conditions for the turbulence variables must be separately imposed using NODAL_BOUNDARY_CONDITION commands. Wall roughness may be modeled by specifying an average wall roughness height for equivalent sand grains, given by roughness_height.
In some circumstances it is necessary to "turn off" or "deactivate" a previously-defined turbulence boundary layer wall. This is accomplished by setting the active flag through active_type. A value of all is the default and means that all surfaces in the set are active (active flag = 1) as turbulence boundary layer walls. A value of none means that no surface is active (active flag = 0).
- The surface is not in any INTERFACE_SURFACE set; active flag = 1.
- The surface is in an INTERFACE_SURFACE set, but it does not find a contact surface; active flag = 1.
- The surface finds a contact surface of fluid medium; active flag = 0.
- The surface finds a contact surface of solid/shell medium; active flag = 1.