istft
Inverse Short-Time Fourier Transform.
Syntax
x = istft(x)
x = istft(st,fs)
x = istft(st,fs,window)
x = istft(st,fs,window,overlap)
x = istft(st,fs,window,overlap,nfft)
x = istft(st,fs,window,overlap,nfft)
x = istft(st,fs,window,overlap,nfft,range)
[st,t] = istft(...)
Inputs
- st
- The short-time fourier transform input, with segments stored by column.
- window
- The window size, or the window column vector.
- overlap
- The number of overlapping points in adjacent windows.
- nfft
- The size of the (two-sided) fft.
- fs
- The sampling frequency.
- range
- The spectrum type. The options are as follows:
- 'onesided'
- 'twosided' (default)
Outputs
- x
- The generated time domain signal.
- t
- The vector of times corresponding to the start of each column of st.
Example
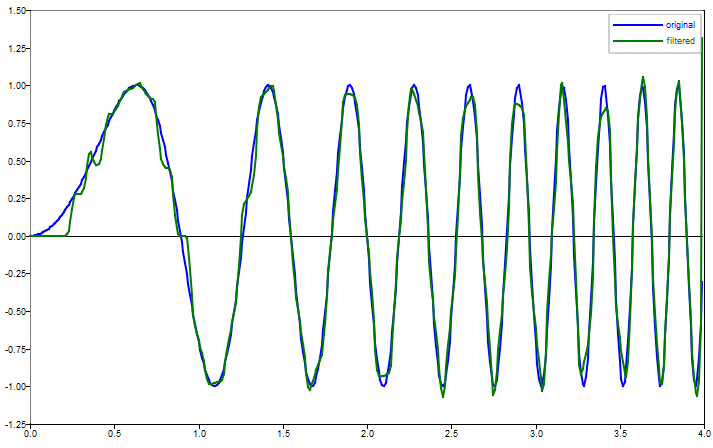
Use stft/istft to remove frequency components with low magnitudes from a linear chirp signal.
f0 = 0;
f1 = 5;
T = 4;
c = (f1 - f0) / T;
t = [0:0.01:T-0.01];
x1 = sin(2 * pi * ((c/2)*t.^2 + f0*t));
[st, t_st, f] = stft(x1, 100, 20, 10, 32, 'onesided');
idx = (abs(st) > 2.5);
st = st .* idx;
x2 = istft(st, 100, 20, 10, 32, 'onesided');
plot(t, x1);
hold on;
plot(t, x2);
legend('original', 'filtered');
Comments
stft and istft are not true inverses. Once the spectrum is modified in some way there may be no time signal that exactly corresponds to it due to overlap. The time signal produced is a least squares fit based on analysis in the following paper: Daniel W. Griffin and Jae S. Lim "Signal Estimation from Modified Short - Time Fourier Transform", IEEE 1984, 10.1109.
Default values are assigned to arguments with a [] input.
The fs, window, overlap, nfft, and range inputs should correspond to those used when calling stft.
With no return arguments the function will automatically plot the result.
The window type and overlap should be chosen to meet the constant-overlap-add (COLA) criterion. Examples of this include the Hann window when overlapped by 1/2 or 2/3.