filter
Filter a signal with an IIR or FIR filter.
Syntax
y=filter(b,a,x)
y=filter(b,[],x)
y=filter(b,a,x,[],dim)
Inputs
- b
- The numerator polynomial coefficients of the filter.
- a
- The denominator polynomial coefficients of the filter.
- x
- The signal to be filtered. If x is a matrix, then each column is filtered.
- dim
- The dimension on which to operate.
Outputs
- y
- The filtered signal.
Example
Filter a signal with a 100 Hz Butterworth filter using filter.
% define signal
f1 = 62.5;
f2 = 250;
omega1 = 2*pi*f1;
omega2 = 2*pi*f2;
fs = 2000;
ts = 1/fs;
n = 100;
t = [0:ts:n*ts];
signal = sqrt(2) * sin(0.5*omega1*t) + sin(omega1*t) + 0.25 * sin(omega2*t);
% define filter
[a,b] = butter(4,100/(fs/2));
% filter signal and plot
output = filter(a,b,signal);
plot(t,signal);
hold on;
plot(t,output);
legend('raw signal', 'filtered signal');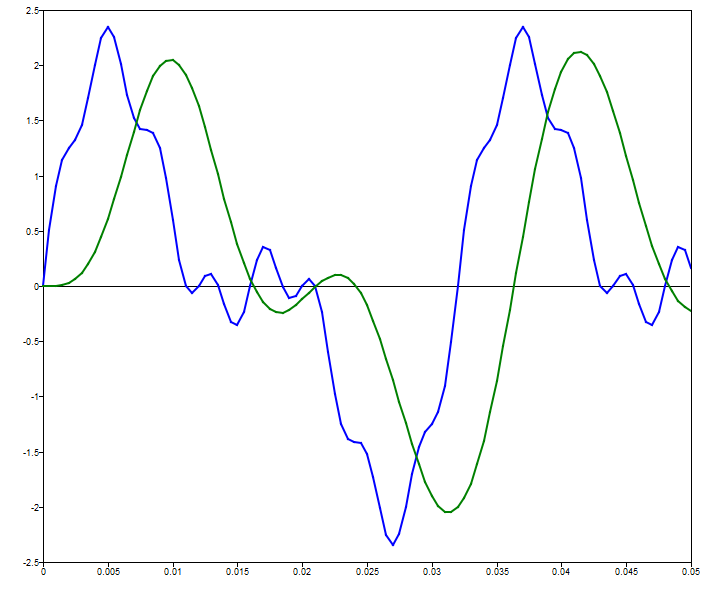
Comments
An infinite impulse response (IIR) filter has both a numerator and a denominator. A finite impulse response (FIR) filters has only a numerator, so its denominator is specified as [].
When specifying dim, the fourth argument should be []. It is a placeholder for the initial conditions, which are not yet supported.