Loading [MathJax]/jax/output/CommonHTML/jax.js

ヘルプ
新機能
SimSolid 2025の新機能に関する情報。
はじめに
基本について学習し、ワークスペースを理解します。
チュートリアル
SimSolidに関するインタラクティブなチュートリアル。
外部製品とのインターフェース
SimSolidの出力ファイル形式をサポートするインターフェース。
ジオメトリ
SimSolidでのジオメトリエンティティの扱いとプロパティに関する情報。
アセンブリ
モデルでパートのプロパティと動作を定義するために使用できる機能のサマリー
結合
結合を使用して、アセンブリのパート間で関心領域の関連付けを定義します。
解析の作成
プロジェクトで使用する解析を作成します。
境界条件
SimSolidに用意されている各種境界条件。
ポスト処理
解析の実行とSimSolidでの結果表示および評価。
設計スタディ
設計スタディを使用すると、複数の設計シナリオの構造性能を効率的に評価して比較できます。
検証問題
検証モデル。
- 概要
  SimSolid検証問題ドキュメントの目的と形式。
- モデルファイルへのアクセス
  目的とするモデルファイルにアクセスしてダウンロードする方法を学びます。
- 静解析
- 固有値解析
- 熱解析
- 熱荷重
- 非線形
  - SS-V：5000 連成解析 - 熱負荷下のバイメタル梁
    テスト番号VNL01 梁の材料界面の温度と最大たわみ量を求めます。
  - SS-V：5010 Z字型片持ち梁
    テスト番号VNL02 大きさが変動する横荷重の下でのZ字型片持ち梁の垂直変位を求めます。
  - SS-V：5020 直角フレームの横座屈
    テスト番号VNL03 直角の形状における薄肉フレームのような構造の座屈と座屈後の解析を実行します。
  - SS-V：5030 軸方向に荷重がかかっているプラスチックバーの両端の反力
    テスト番号VNL04 塑性限界を超えて軸方向に荷重がかかっているバーの固定された両端の反力と最大変位を求めます。
  - SS-V：5040 軸方向に荷重がかかっているプラスチックバーの残留変形
    テスト番号VNL05 塑性限界を超えて軸方向に荷重がかかっているバーの残留変形を求めます。
  - SS-V：5060 梁の分離
    テスト番号VNL07 適用された荷重に応じて全体または部分的な梁の分離 / 滑りを求めます。
  - SS-V：5070 ピンチされた半球シェル
    テスト番号VNL08 内向きおよび外向きの集中力荷重がかかった半球シェルの変位を求めます。
  - SS-V：5080 剛体パンチ塑性
    テスト番号VNL09完全塑性材料と等方的硬化材料に対する大きなブロックに押し付けられたパンチの反力を求めます。
  - SS-V：5090 ブッシング剛性
    テスト番号VNL10 長さに沿って10 N-mのモーメントを受ける円筒の回転を求めます。
- 動解析
- 疲労
- 複合材料
よくある質問
このセクションでは、以下に関する代表的な質問とよくある質問に対する回答を紹介します。

SS-V：5030 軸方向に荷重がかかっているプラスチックバーの両端の反力

テスト番号VNL04 塑性限界を超えて軸方向に荷重がかかっているバーの固定された両端の反力と最大変位を求めます。

定義

Figure 1.

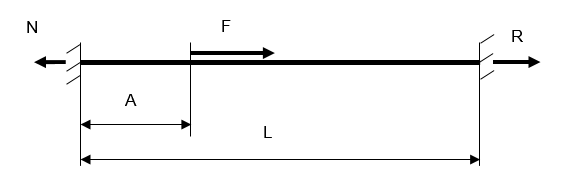
バーの寸法は10 x 10 x 200 mmです。荷重ポイントと左端の間の距離はA=50 mmです。バーの材料のひずみ応力曲線は、べき法則で定義されます：

$σ = K ε^{n}$

ここで、

$K$: 強度係数
$n$: [0,1]の範囲内にある必要があります

$n$ =0

材料は完全にプラスチックです。

$n$ =1

材料は弾性です。

材料特性は以下の通りです：

特性: 値
$K$: 530 MPa
$n$: 0.26
ポアソン比: 0

Figure 2. 対応するひずみ応力曲線

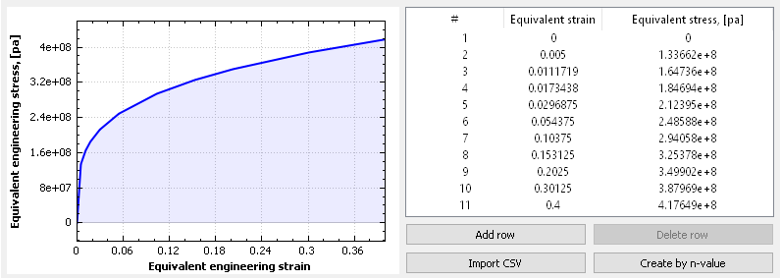
このスタディは、荷重F値30000 N、47000 N、55000 N、および60000 Nに対して実行されました。これらの荷重は、バーの弾性プラスチック応答のすべての範囲をカバーしています。

基準解

ここでは、1次元の解析基準解について説明します。

バーの長さは、荷重下では変化しません。

$\int_{0}^{A} ε 1 d x - \int_{0}^{L - A} ε 2 d x = 0$

または

$\int_{0}^{A} \sqrt[n]{N / (K * A)} d x - \int_{0}^{L - A} \sqrt[n]{(F - N) / (K * A)} d x = 0$

ここで、

$ε 1$: バーの左スパンでの引張ひずみ。
$ε 2$: バーの右スパンでの圧縮ひずみ。
$N$: バーの左端での反力。
$R = F - N$: バーの右端での反力。
$A$: バーの断面積

この式から、バーの左端での反力を求めることができます。

$N = F / (1 + {(a / b)}^{n})$

また、右端では次のようになります： $R = F - N$

結果

バーを、両端が完全拘束された3Dソリッドとしてモデル化しました。ソリッドバー軸では軸力Fを正確に適用できませんでした。そのため、バーのサイドに4つのラインスポットを作成し、合計荷重Fをこれらのスポット上に均等に分配しました（図 3）。

Figure 3.

以下の表は、反力の結果をまとめたものです。


力 F [N]	SOL基準、反力 [N]	SimSolid、反力 [N]	%差異
30000	17128	17522	2.3%
47000	26834	26987	0.5%
55000	31401	31660	0.8%
60000	34256	34490	0.6%