ローターダイナミクス解析
理論
ローターダイナミクスは、シャフト、タービン、コンプレッサーなど、回転機械の挙動に関する動的構造解析です。この解析フレームワークは、ローターの動的応答を正確にモデル化し、予測するための主要な理論的概念を組み込んでいます。構造内のコンポーネントが回転すると、ジャイロ力や円運動減衰力などの力が付加的に作用します。
システムにおける回転するコンポーネントの影響を判断することが重要です。回転するコンポーネントによりモデルにジャイロ力が作用する場合、通常、システムの固有振動数は変化します。回転するコンポーネントによる円運動減衰力によって、システムが不安定になる可能性があります。これらの力は、回転するコンポーネントの周波数の関数となります。構造内で回転するコンポーネントは、ギアが取り付けられているシャフトです。ローターとその角周波数の設計は、構造の動的応答に影響する可能性があります。どのような設計でも、ローター軸を中心として非対称な質量分布になりがちです。このような不均衡な質量は、それがわずかであっても、さまざまな要因によってローターの変形をもたらす可能性があります。これらの変形の大きさは、シャフトの回転速度が構造の固有振動数と等しくなると拡大し(共振)、システムの破壊的故障を引き起こす可能性があります。
ローターダイナミクス解析は、旋回速度(ローターの質量中心が回転軸の周りを回る周波数)とローターの回転速度(Ω)との関係に基づいて分類できます。
SimSolidによるローターダイナミクスモード解析では、多くの場合、複素固有値解析により、主に非同期アプローチを用いて、ローター速度の関数として前方および後方の旋回周波数を計算します。これによりキャンベル図を作成できます。旋回速度は、ローターの回転速度とは独立しています(ω≠Ω)。このアプローチは、旋回固有振動数(固有振動数)を求めるために使用されます。これは、キャンベル図をプロットして臨界速度を特定し、潜在的な不安定性を調査するために不可欠です。
コリオリ効果
- 回転するローターでは、振動による質点の半径方向速度(Vr)により接線方向のコリオリの力が生じ、同様に、接戦方向の速度(Vt)により半径方向のコリオリの力が生じます。
- この効果は、運動方程式のジャイロマトリックスによって捉えられ、これによりx方向とy方向の運動が連成して前方および後方のそれぞれの旋回モードが生じます。
応力硬化(遠心剛化)
- ローターが回転すると、遠心力によってローター構造に引張応力が生じます。
- この引張応力は、ローターの有効応力を増加させ、その結果、回転速度が上昇すると固有振動数(旋回周波数)がわずかに高くなります。SimSolidのローターダイナミクス定式化では、この効果を考慮して、特に回転速度が速い場合、より正確に臨界速度を予測します。
座標系
SimSolidでは一般的に、ローターダイナミクス解析の定式化に回転座標系を使用します。座標系(x、y、z)は、ローターの回転速度(Ω)でローターと共に回転します。この座標系では、ジオメトリは静止しているため、不均衡など、モデルの一部の側面を簡素化できます。この選択により、ロータージオメトリのモデル化が簡素化され、回転の影響を容易に運動方程式に含めることができるようになります。
キャンベル図
- これは、ローターの回転速度(Ω、単位はrad/sまたはHz)に対するローターシステムの旋回固有振動数(固有振動数、ω、単位はrad/sまたはHz)のプロットです。
- 臨界速度は、固有振動数のラインがローター速度のライン(Ω = ω、すなわち1Xライン)およびその倍数成分(2Xラインなど)と交差するポイントとして特定されます。
- 1Xとの交差が最も重要で、ここでは、旋回周波数が質量の不均衡による励振振動数と一致し、共振を引き起こして過度な振動が生じる可能性があります。
Figure 1. 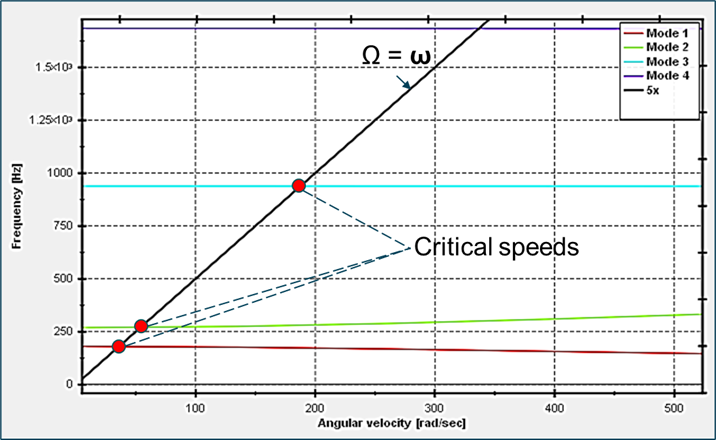
- 1Xとの交差が最も重要で、ここでは、旋回周波数が質量の不均衡による励振振動数と一致し、共振を引き起こして過度な振動が生じる可能性があります。
減衰図
- これは、ローターの回転速度(Ω)に対する減衰(通常、固有値の実部を固有値の虚部で割り、それに2を掛けたもの)をプロットしたものです。
- 安定性評価:
- 正の減衰は、ローターシステムが安定しており、振動が時間の経過と共に減衰することを意味します。
- 負の減衰は、ローターシステムが不安定で、振動の振幅が時間の経過と共に増大し、故障を引き起こす可能性があることを意味します。これは、オイルホイップや内部摩擦などの不安定性メカニズムの発生に関係することがよくあります。