Acoustic Infinite Elements
Acoustic modeling in finite and semi-infinite domains is essential in the prediction of quantities such as external and radiated noise in vibro-acoustic problems. Infinite elements are a popular way of modeling these domains.
- Direct and Modal Frequency Response Analysis
- Direct and Model Transient Response Analysis (via Fourier Transformation)

Implementation
Considering the domain in the figure above, the region surrounding the structure (shaded area) is modeled using a conventional fluid FE mesh, and the far field is modeled using infinite elements defined on a 2D interface between the finite and infinite (unbounded) domains.
The governing equations for frequency response are given below. The following equations are solved for the pressure .
- Wave number
- Circular frequency
- Speed of sound
- Unit normal to the surface of the fluid elements
- Unit normal to the surface of the "infinite boundary" (sufficiently far away from the structure)
- Pressure
- Fluid density
- Displacement of the structural boundary in the direction
Input/Output
Input
- Fluid material properties (bulk modulus, speed of sound, fluid density) can be specified for the fluid elements on the MAT10 Bulk Data Entry.
- Pole location (origin of the acoustic disturbance). Pole is the center of acoustic disturbance. This can be defined on the PACINF Bulk Data Entry via the XP, YP, ZP coordinates.
- The nodes defining the interface between the infinite and semi-infinite domain. This is defined as the Infinite elements (currently 3-noded CACINF3 and 4-noded CACINF4 elements are supported).
- The radial interpolation order can be specified via the RIO field on the PACINF entry.
Modeling Guidelines
- A minimum of 1 layer of Fluid elements should be defined on the surface of the structural domain of interest.
- The Infinite elements (CACINF3 and CACINF4) should only be defined on the topmost surface of the Fluid elements.
- Infinite Elements modeling practice can be typically recommended as:
Figure 2. Modeling Practices for Infinite Elements . (Green elements: Infinite Elements, Red arrow indicates direction of the receiver (semi-infinite domain), Blue Elements: Acoustic elements) 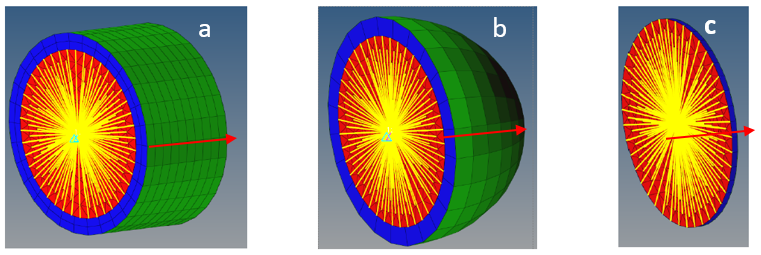
Correct Modeling Practices- In Figure 2(a), infinite elements are on the skin of the fluid acoustic elements covering both sides (front and lateral) in the direction of the receiver.
- In Figure 2(b), infinite elements are on the skin of the fluid acoustic elements covered through curved surface in the direction of the receiver.
Incorrect Modeling Practices:- In Figure 2(c), infinite elements are the skin on the fluid acoustic elements covering one of the sides (front side) in the direction of the receiver.
- Normals of infinite elements should always point away from the pole.
- Sound pressure can be measured on the receiver grid points. For visualization of the sound pressure contour, the receiver grids should be connected using PLOTEL elements. See the Output section below for more information.
- Source is generally a structure which is excited by a load, which also can be fluid grid with SLOAD.
Modeling Checklist
- There should be at least 4 infinite elements per wavelength of the acoustic wave
associated with each of the loading frequencies. In other words, the characteristic size
of the infinite element, h is given
by:Note: If this criterion is not satisfied, a warning will be issued in the .out file.
- An appropriate RIO should be specified in the PACINF card. The further the far-field microphone locations from the pole, the higher the RIO should be for more accurate results. Again, caution should be exercised as a higher RIO may cause ill-conditioning in the system matrices. It is recommended to start from the default value (5) and increase the RIO until the results are satisfactory or have converged.
- The pole is the source/origin of the acoustic disturbance. For vibro-acoustic
problems, a good starting point for the choice of the pole is the centroid of the
structural part(s). For a more accurate pole location, one can enclose the structure(s)
using panels (‘n’ panels) and request ERP outputs. Once this is known, the x-location
for the pole may simply be obtained from the x-locations of the geometric centers (
) of the panels.
Similar expressions hold for the y and z coordinates of the pole.
- While using modal frequency response, the modal space must contain enough modes so as to capture the mechanics of the structure and acoustic cavity appropriately. A good starting point for the upper-bound in the EIGRL/EIGRA Bulk Data Entry is about 2 to 2.5 times the maximum frequency. It is also your responsibility to ensure convergence with regard to the number of modes.
- In accordance with the modeling guidelines, exterior acoustics is appropriately simulated by enclosing the entire structure with an acoustic cavity mesh and further adding a layer of infinite elements on this acoustic cavity mesh. The surface of the acoustic cavity mesh on which the layer of IE exists should be as smooth as can be allowed without any discontinuities.
- Pressure output calculations at far-field locations should be correctly requested by ensuring that the GRID entry at the microphone location belongs to the domain of the acoustic media (CD entry = -1).
- The generations of the interface between the fluid and structure and the rigid fluid interface (at any acoustically rigid boundaries) should be verified. This is output just after starting an OptiStruct run in the .interface file and can be quickly loaded into HyperMesh to visualize the interfaces.
- The material properties in the MAT10 card referenced by the
PACINF entry should have entries that have units that are
consistent with the existing structural model.
For example, kg-m-s (SI) or Ton-mm-s.
- You can also verify the results of the analysis by ensuring the results between direct and modal frequency response are in close agreement.
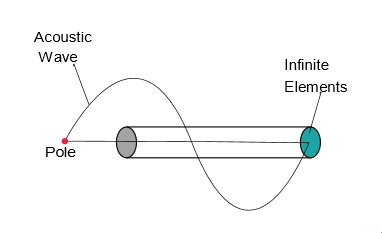
- For some geometries of the finite domain (that includes the structure and acoustic
cavity region, for example, the domain enclosed by the layer of infinite elements), the
distance between the pole to the interface should allow for the propagation of one
acoustic wavelength (Figure 3). This simply means.
Output
Currently only Pressure output is supported for any grid points in the acoustic domain using Infinite Elements. The Pressure output can be requested using the DISPLACEMENT I/O Options Entry. Pressure output is available for Acoustic Direct and Modal Frequency Response Analysis and in the time domain for Direct and Modal Fourier Transient analysis analyses.
The Pressure output can be requested using the DISPLACEMENT I/O Options Entry. Pressure can be requested for grid points belonging to the fluid domain of the model at external microphone locations which can be specified as GRID point sets. This is supported for H3D and PUNCH file formats.