Specify Pre-Load in your Flexible Components

The ANCF formulation in MotionSolve lets you specify two sets of positions for each grid that makes up the flexible component:

The model or loaded configuration. This set of nodal coordinates defines the loaded or model configuration. In this configuration, you can specify the following:

The position vector at the loaded/stressed configuration

$\underline{r} = x \hat{i} + y \hat{j} + z \hat{k}$

The gradient vector in X direction at the loaded/stressed configuration

${\vec{r}}_{x} = {(\frac{\partial \vec{r}}{\partial x})}_{x} \hat{i} + {(\frac{\partial \vec{r}}{\partial x})}_{y} + \hat{j} {(\frac{\partial \vec{r}}{\partial x})}_{z} \hat{k}$

The gradient vector in Y direction at the loaded/stressed configuration

${\vec{r}}_{y} = {(\frac{\partial \vec{r}}{\partial x})}_{x} \hat{i} + {(\frac{\partial \vec{r}}{\partial x})}_{y} + \hat{j} {(\frac{\partial \vec{r}}{\partial x})}_{z} \hat{k}$

The gradient vector in Z direction at the loaded/stressed configuration

${\vec{r}}_{z} = {(\frac{\partial \vec{r}}{\partial x})}_{x} \hat{i} + {(\frac{\partial \vec{r}}{\partial x})}_{y} + \hat{j} {(\frac{\partial \vec{r}}{\partial x})}_{z} \hat{k}$
The unloaded or relaxed configuration. This set of nodal coordinates defines the unloaded or relaxed configuration. These are denoted in the ANCF XML file by a suffix "0" after each attribute, for example, x0, y0, z0 and so on. In this configuration, you can specify the following:

The position vector at the unloaded/relaxed configuration

$\vec{r} 0 = x θ \hat{i} + y θ \hat{j} + z θ \hat{k}$

The gradient vector in X direction at the unloaded/relaxed configuration

${\vec{r}}_{x 0} = {(\frac{\partial \vec{r}}{\partial x})}_{x 0} \hat{i} + {(\frac{\partial \vec{r}}{\partial x})}_{y 0} + \hat{j} {(\frac{\partial \vec{r}}{\partial x})}_{z 0} \hat{k}$

The gradient vector in Y direction at the unloaded/relaxed configuration

${\vec{r}}_{y 0} = {(\frac{\partial \vec{r}}{\partial x})}_{x 0} \hat{i} + {(\frac{\partial \vec{r}}{\partial x})}_{y 0} + \hat{j} {(\frac{\partial \vec{r}}{\partial x})}_{z 0} \hat{k}$

The gradient vector in Z direction at the unloaded/relaxed configuration

${\vec{r}}_{z 0} = {(\frac{\partial \vec{r}}{\partial x})}_{x 0} \hat{i} + {(\frac{\partial \vec{r}}{\partial x})}_{y 0} + \hat{j} {(\frac{\partial \vec{r}}{\partial x})}_{z 0} \hat{k}$

Note: If the unloaded/relaxed configuration is not specified, MotionSolve assumes that the loaded configuration is identical to the unloaded configuration, thereby the structure is not pre-stressed. This is also the case if the unloaded configuration is identical to the loaded configuration.

As an example, consider a beam of circular cross section fixed at both its ends and subjected to a center load. The unloaded configuration is specified as the configuration when the load is not present or equal to zero.

Figure 1. The Unloaded or No Load Configuration

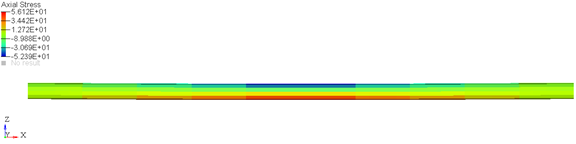
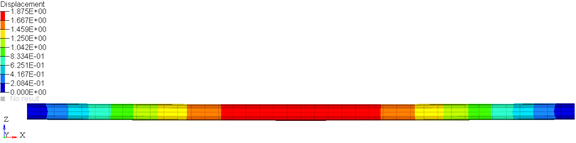
The loaded configuration (Figure 2) is specified as the configuration when the beam is under maximum deformation. A center load of 1000N is applied in this case.

Figure 2. The Loaded Configuration. Shown here are the displacement contours.

Thus, the loaded and unloaded configurations in the ANCF XML file are specified as follows (this is illustrated for the middle grid, in the interest of saving space):

<GRID
   id="301008"
   x0="500.000000"  y0="0.000000" z0="0.000000"
   rx0="1.000000 0.000000 0.000000"
   ry0="0.000000 0.000000 1.000000"
   rz0="0.000000 -1.000000 0.000000"
   x="5.0000000E+02" y="2.2342947E-09" z="-1.8751877E+00"
   rx="1.0000086E+00 1.8714474E-15 1.4090006E-17"
   ry="-1.3419917E-17 -1.2981139E-09 9.9999766E-01"
   rz="1.8569096E-15 -9.9999740E-01 -1.3584520E-09"
/>

As can be seen, the loaded and unloaded nodal coordinates are different. The difference between the loaded and unloaded "z" positions represents the maximum deformation of this beam in this case.

This method can thus be used to represent pre-stressed components in your model. For such scenarios, MotionSolve calculates the stress in the component based on the difference between the loaded and unloaded configuration, which can be used to model pre-stress in the flexible component. For the component defined above, the "pre-stress" in the beam at t=0 is illustrated in Figure 3.

Figure 3. The Stress at t=0 Calculated Due to the Difference in Loaded and Unloaded Configurations. Shown here are the axial stress contours.