Forces, Joints and Motions with NLFE Bodies
- 3D/2D generic contact is currently not supported.
- Point to deformable surface contacts and constraints are also not supported
- Distributed force application on the NLFE components is not supported
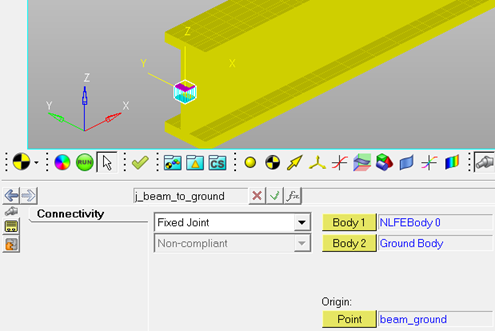
All the other supported force, joint and motion types are applied to the NLFE component via the use of markers. For example, consider the case where an NLFE cantilever beam is fixed to the ground at one end (Figure 1). A fixed joint is created between one end of the beam (NLFEBody 0) and the ground (Ground Body). In doing so, a marker is automatically created and attached rigidly to the NLFE body at the point of attachment (beam_ground).
- Degree of Freedom of the grid
- Constrained?
- Rigid translation of the grid along X axis
- Yes
- Rigid translation of the grid along Y axis
- Yes
- Rigid translation of the grid along Z axis
- Yes
- Rigid rotation of the grid about X axis
- Yes
- Rigid rotation of the grid about Y axis
- Yes
- Rigid rotation of the grid about Z axis
- Yes
- Deformation (axial strain) along X axis
- No
- Deformation (axial strain) along Y axis
- No
- Deformation (axial strain) along Z axis
- No
- Deformation (shear strain) in XY plane
- No
- Deformation (shear strain) in YZ plane
- No
- Deformation (shear strain) in ZX plane
- No
- Rigid translation of the grid along X axis
- No
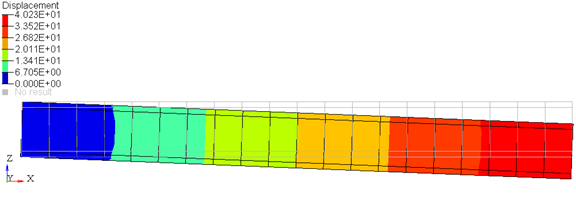
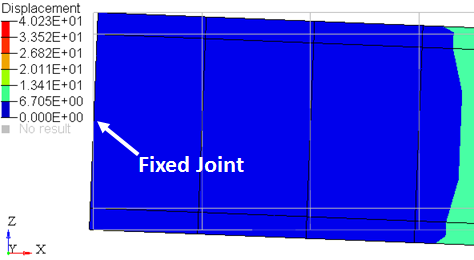
Looking closely at the end where the beam is fixed to the ground (Figure 2), it seems that the beam cross-section has rotated about the Y axis. This seems to be the wrong behavior, since the beam was fixed to ground and so should not rotate about any axis.
The reason the beam appears to rotate about the Y axis in this case is because of the additional 6 DOFs that are not constrained by the fixed joint. Due to this, the gradient vectors of the beam at the fixed end are free to stretch and twist relative to each other. This can be confirmed by plotting the gradient vectors at the start of the beam in the direction along the beam and normal to it.

As can be seen from the plot above, the gradient vector along the beam changes from (1,0,0) to ~(0.998574, 0, -0.0466717). Since the NLFE elements are drawn such that the gradient vector along the beam axis is always normal to the element, this results in what looks like a rotation of the beam cross section at the start.
To alleviate this, you need to "fully" clamp the grid at the fixed end of the beam to the ground. This is achieved by using the CONN0 element. The CONN0 element is a connector element that allows you to rigidify the gradient vectors of a single grid. Please see the NLFE reference manual for more information on this.
For this model, adding the CONN0 element, and "fully" clamping the grid at the fixed end of the beam to the ground results in the expected simulation result shown in Figure 4 below.
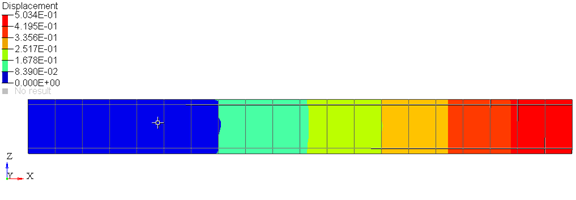
Further, the gradient vectors at the fixed end also do not change during the simulation, as is expected while fixing the beam to the ground at this end.
