Problem 13: Hollow Circular Beam under a Twist Load
Model Description
Model location: <altair>\utility\mbd\nlfe\validationmanual\model1.mdl
This model consists of a straight cantilever beam of a hollow circular cross-section. The beam is subjected to a torsion load at its endpoint as shown in Figure 1 below.

- Twist angle
- Shear strain
- Beam length
- Beam radius.
- Polar moment of inertia about the beam axis.
- Shear modulus
- Young's modulus
- Poisson ratio
Multibody Model
The cantilever beam is modeled using 10 NLFE beam elements in MotionSolve. NLFE beam elements with a hollow tube section are used by specifying an inner and outer radius. The cantilever beam is fixed to the ground by a fixed joint. Gravity is turned off for this model.
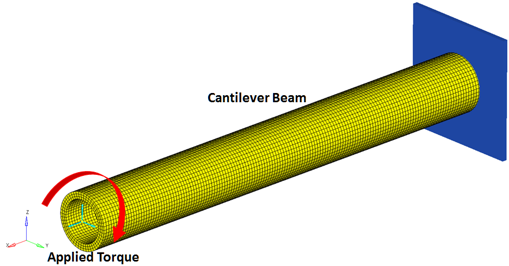
A torque is applied at the end of the cantilever beam using a TorqueOnly Force_Vector_OneBody element. A torque of 3x107 Nmm is applied gradually, via a STEP function as:
θ = 0.026686rad

This model is simulated with an end time of five seconds, for a dynamic analysis. Under the end torsion, the beam is expected to twist about its axis by an amount predicted by the theoretical model.
- 1000 mm
- 45 mm
- 60 mm
- 1.392 x 107 mm4
- 8.076 x 104 N/mm2
- 2.1 x 105 N/mm2
- 0.3
Numerical Results
The multibody model described in the previous section is run for an end time of 5.0 seconds. The output request is plotted below.

The twist angle for the numerical result is found as:
Conclusion
The NLFE model with 10 NLFE beam elements shows close agreement to the theoretical results for this case.
| Beam Theory | Numerical | % error | |
|---|---|---|---|
| Twist Angle | 0.026686 rad | 0.026690 rad | 0.02 % |