Résolution d'un système différentiel du 1er ordre : la méthode d'Euler
Système différentiel du 1er ordre : écriture
L'application de la méthode des Eléments Finis à des problèmes aux dérivées partielles de type parabolique ou hyperbolique conduit à la résolution de systèmes différentiels du premier ordre du type :
où M et N sont
des matrices régulières
Par quelques transformations algébriques, ce système peut être mis sous la forme :
(1)
Discrétisation
Le principe commun à toutes les méthodes numériques consiste à discrétiser l'intervalle de temps [t0, tmax] en pas de temps Δt.
La dérivée de X(t) peut être approchée par une différence entre deux valeurs successives de X :
(2)
Méthode de la tangente
La plus simple des méthodes numériques, appelée méthode de la tangente, consiste à remplacer dans le système (1) la dérivée dX/dt par l'approximation précédente (2).
L'équation (1) s'écrit alors :
d'où la solution approchée aux points ti+1 = t0 + ih :
|
|
Cette méthode est appelée méthode de la tangente car elle consiste, sur une équation unidimensionnelle à déterminer le point (ti+1, Xi+1) en menant à partir du point (ti, Xi) la tangente à la courbe solution.
Méthode de la tangente (suite)
La méthode de la tangente, agréable par sa simplicité requiert cependant le choix d'un pas de temps h très petit pour assurer une précision convenable à la solution. L'influence de la taille du pas de temps sur la précision est présentée sur la figure ci-dessous.
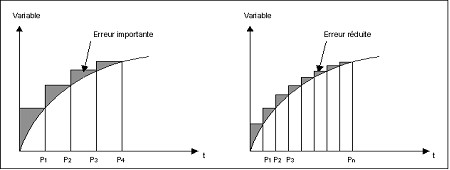
Méthodes explicites / implicites
On préfère, à la méthode de la tangente, des méthodes plus sophistiquées, qui en augmentant la précision, permettent de choisir des pas de temps plus élevés, et donc de limiter le volume de calcul.
Ces méthodes ne sont pas détaillées dans ce document. Quelques éléments d'information sont proposés dans les deux tableaux ci-dessous.
| Méthode … | Description | |
|---|---|---|
|
dite « à pas séparés » ou explicites |
l'approximation de X à l'instant ti+1 ne fait intervenir que des variables connues à l'instant ti |
La dérivée est calculée avec les deux pas précédents :
|
|
dite « à pas liés » ou implicites |
l'approximation de X à l'instant ti+1 fait intervenir les valeurs que X prend à ce même instant |
La dérivée est calculée avec le pas courant et le précédent :
|
| Les méthodes … | Avantage | Inconvénient |
|---|---|---|
| … explicites | sont plus faciles à mettre en œuvre … |
mais nécessitent souvent le choix d'un pas de temps h très petit à cause du phénomène d'instabilité numérique |
| … implicites | sont plus stables et autorisent donc des pas de temps plus grands | mais nécessitent à chaque pas de temps un volume de calcul élevé à cause du terme implicite |
Méthodes semi-implicites
Dans ces méthodes, on introduit un coefficient θ compris entre 0 et 1 et l'on approxime l'équation par :
où 
Les valeurs de θ qui définissent les schémas les plus utilisés sont données dans le tableau suivant :
| Valeur de θ | Nom du schéma |
|---|---|
| 1 | implicite |
| 0.878 | Liniger |
| 2/3 | Galerkine |
| 1/2 | Crank-Nicholson |
| 0 | explicite |
Les méthodes semi-implicites sont inconditionnellement stable pour θ ≥ 0.5. Le schéma le plus utilisé est celui dit de Crank-Nicholson qui pour θ = 1/2 assure la stabilité en permettant une excellente précision.
Dans Flux
L'équation temporelle résolue est une équation différentielle du premier ordre. Elle est intégrée par une méthode implicite. Toutes les grandeurs sont donc calculées pour la valeur finale du pas de temps.