Aspect théorique et cadre de la méthode
Introduction
Cette section donne quelques éléments de principe pour expliciter la base théorique utilisée en interne pour calculer un critère d'erreur.
Principe de la méthode
Flux met à disposition 2 méthodes qui peuvent être complémentaires pour déterminer l'erreur d'une solution.
Une première méthode de calcul de l'erreur est basée sur les équations de conservation des grandeurs physiques tel que la conservation de l'énergie, la conservation du Flux magnétique ou encore la conservation du Flux de chaleur pour les applications thermiques.
Une seconde méthode est basée sur des variations rapides (gradient) de la co-énergie locale. Moins physique, cette dernière méthode part du postulat que plus les grandeurs d'énergie varient sur un élément fini, plus l'erreur est importante.
Quelle que soit la méthode utilisée, le principe de calcul consiste à vérifier localement chacune de ces équations dans chaque élément. Cela permet également de visualiser quelles sont les zones ou l'erreur est la plus grandeur, et de réaliser globalement à chaque région un bilan de l'erreur qui donne des éléments de comparaison entre différentes solutions.
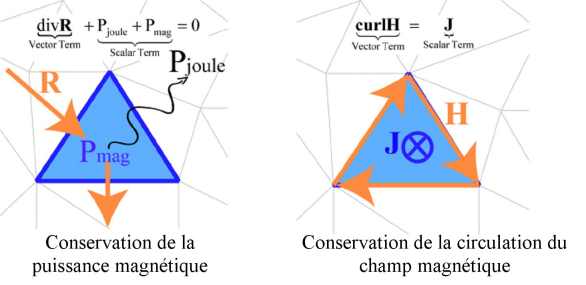
Les équations de conservation pour Flux
En électromagnétisme, différentes lois de conservation doivent être assurées. Pour Flux, ces équations sont :
- L'équation de conservation du courant :
div(J) = 0
où J est le vecteur densité de courant.
- L'équation de conservation du flux magnétique :
div(B) = 0
où B est le vecteur densité d'induction magnétique.
- L'équation de Maxwell Gauss :
div(D) = 𝜌
où D est le vecteur densité d'induction électrique et 𝜌 la densité volumique de charge.
- L'équation de conservation de la puissance :
où E×H est le vecteur densité de puissance électromagnétique, J•E est la densité volumique de pertes Joule et la densité volumique de puissance magnétique.
- L'équation de conservation du flux thermique :
div(Jt) = q
où Jt est le vecteur densité de flux thermique et q la densité volumique de chaleur.
Les équations de variation de la co-énergie
Les 2 critères nommés gradient de la co-énergie magnétique et gradient de la co-énergie électrique sont basés sur l'étude de la variation locale de la co-énergie.
- Gradient de la co-énergie magnétique :
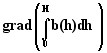
- Gradient de la co-énergie électrique :
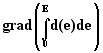
Références
Pour aller plus loin, veuillez vous référer à la publication suivante :
Rondot L. , Mazauric V., Wendling P., « An Energy-Compliant Magnetodynamic Error Criterion for Eddy-Current Calculations », IEEE Trans. Magn., June 2010, Vol. 46 issue 6 p. 2353 – 2356