Morris Parallel Rotating Tube

Description

A duct flow correlation to be used with tubes that are rotating, parallel to the axis of rotation, and offset from the axis of rotation.

Type: Mixed Laminar-Turbulent Duct Nu
Subtype: Morris Parallel Rotating Tube

Table 1. Inputs List
Index	UI Name (.flo label)	Description
1	Flow Element (FLOW_ELM)	The ID for the flow element that will be used for the mass flow rate and other correlation inputs. If AUTO, the correlation must be applied to a convector that is connected to a fluid chamber that has only one flow element entering this chamber. The ID of this flow element is used. The element can be of almost any type, although some types do not have geometric inputs that can be obtained with the AUTO option of the remaining inputs.
2	Hydraulic Diameter (HYD_DIA)	Passage hydraulic diameter. If AUTO, the hydraulic diameter of the flow element from input 1 is used.
3	Flow Area (FLOW_AREA)	Passage flow area. If AUTO, the area of the flow element from input 1 is used. If the area from the flow element is not available, the passage is assumed circular, and the hydraulic diameter is used to calculate the area.
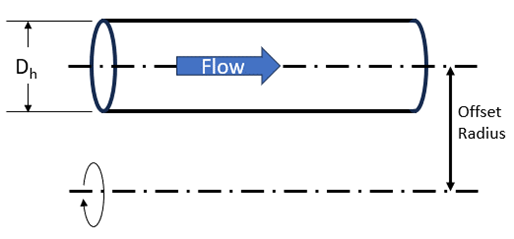
4	Offset Radius (OFFSET_RAD)	Distance from the rotation centerline to the tube centerline. If AUTO, the radius of the flow element from input 1 is used.
5	Tube Rotation Index (ROTOR_IDX)	The index of the rotor shaft containing the RPM for this tube. The speed for this rotor shaft is set in the Run > Reference Conditions tab. If AUTO, the rotation of the flow element from input 1 is used or an RPM associated with the surface thermal node is used.
6	HTC Multiplier (HTC_MULT)	A constant multiplier to scale the value of the heat transfer coefficient obtained from the correlation.

Formulation

This correlation uses a Nusselt number equation by Morris (reference 1) for a fully developed turbulent flow and a Nusselt number equation by Wood (reference 2) for a laminar flow. A linear interpolation is used if the Re is in the transitional regime. The turbulent Nu is not allowed to be lower than a no rotation duct flow Nu using Gnielinski’s correlation.

Axial Reynolds number:

R e = \frac{\dot{m} D_{h}}{A r e a μ}

Rotational Reynolds number, J:

J = \frac{ω ρ D_{h}^{2}}{μ}

Rotational Rayleigh number, Ra:

R a = \frac{H ω^{2} β (T_{g a s} - T_{w a l l}) D_{h}^{3} ρ^{2}}{8 * μ^{2}} P r

H = O f f s e t R a d i u s

For Re <= RE_LAM (default is 2185)

N u_{0} = 3.66 = n o r o t a t i o n N u

N u_{l a m} = N u_{0} * .262 * {(R a R e P r)}^{0.173}

For Re >= RE_TURB (default is 2415)

N u_{t u r b} = .0089 * R e^{.8} {*J}^{.25}

H T C = \frac{N u * k}{D_{h}} w h e r e k = f l u i d c o n d u c t i v i t y a t f i l m t e m p e r a t u r e

Table 2. Output List
Index	.flo label	Description
1	TNET	Thermal network ID which has the convector where this correlation is used.
2	CONV_ID	Convector ID which is using this correlation.
3	FLOW_ELM	Flow element from input 1 or automatically selected.
4	FLOW	Mass flow rate used in the Re calculation.
5	HYD_DIA	The hydraulic diameter used in the HTC calculations.
6	RE_AX	Axial Reynolds number.
7	RE_ROT	Rotational Reynolds number, J.
8	NU	Calculated Nusselt number.
9	HTC	Calculated Heat Transfer Coefficient.

Heat Transfer Correlation References

Morris, W.D. and Woods, J.L, Heat Transfer in the Entrance Region of Tubes That Rotate About a Parallel Axis, Journal of Mechanical Engineering Science, 20(6), 1978, 319-325.
Woods, J.L and Morris, W.D., A Study of Heat Transfer in a Rotating Cylindrical Tube, ASME Journal of Heat Transfer, Nov 1980, 612-616.