Far Fields
View the quantities and properties that are available for a far field request.
On the Home tab, in the Add results group, click the
![]() Far field icon.
Far field icon.
| Quantity | Properties |
|---|---|
| Electric field | Total |
| Gain | Theta |
| Realised gain | Phi |
| Directivity | Ludwig III (Co) |
| Radar cross section (RCS) | Ludwig III (Cross) |
| LHC | |
| RHC | |
| Axial ratio | Minor / Major |
| Major / Minor | |
| Handedness |
The options available for far fields:
- Total
- The total value independent of the polarisation.
- Theta
- The vertical (or ) component.
- Phi
- The horizontal (or ) component.
- Ludwig III (Co)
- The reference polarisation as defined by Ludwig for conventional measurement configurations.
An antenna that is Z directed implied for which the reference polarisation is
intended along the
cut.
(1) - Ludwig III (Cross)
-
The cross polarisation as defined by Ludwig for conventional measurement configurations. An antenna that is Z directed implied for which the reference polarisation is intended along the .
(2) Conventions for the Ludwig coordinate system are defined by the following parameters:- and
- Rotational angles in the spherical coordinate system as defined in Feko.
- Directional unit vector in the direction.
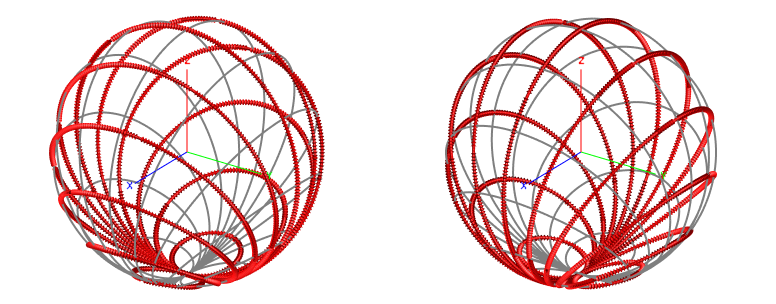
Figure 1. The reference and cross polarisations in 3D space. - LHC
- The left hand circularly polarised component. The polarisation vector rotates counter clockwise when viewed from a fixed position in the direction of propagation.
- RHC
- The left hand circularly polarised component. The polarisation vector rotates counter clockwise when viewed from a fixed position in the direction of propagation.
- Z (+45°)
- When viewed in the direction of propagation, the
unit vector points downwards and the
unit vector to the left. The Z-polarisation vector is
thenwhich lies along an axis rotated +45 degrees from horizontal (in a counter clockwise direction) — coinciding with the direction of the diagonal line of the Z.
(3) - S (-45°)
- The S-polarisation unit vector is which rotated by -45° from horizontal and lies in the direction approximated by the diagonal of the S.
(4) - Minor/Major
- Displays the magnitude of the axial ratio using the axes specification, Minor/Major.
- Major/Minor
- Displays the magnitude of the axial ratio using the axes specification, Major/Minor.
- Handedness
- Displays the sign information for axial ratio on a sphere using different colours for left hand rotating, linear and right rotating fields.