Compose-4030: Optimization Algorithms in OML
Tutorial Level: Intermediate
Compose OML language provides optimization solvers for function minimization and zero finding. The solvers include fminunc for unconstrained minimization, fmincon and ga for constrained minimization, and fsolve for solving systems of nonlinear equations.
This tutorial demonstrates each solver by finding the minimum distance between two non-intersecting ellipsoids defined as follows:
(x-1)2/25 + (y-2)2/16 + (z-3)2/9 = 1
(x-12)2/49 +(y-13)2/81 + (z-14)2/36 = 1
Define the Optimization Problem
Let (x1,y1,z1) be a point on the
first ellipsoid and (x2,y2,z2) be
a point on the second ellipsoid. The goal is to choose the points so that their
distance is minimized. It is more convenient to minimize the squared distance, so we
define the objective function, f, as follows.
f(x1,y1,z1,x2,y2,z2) = (x1-x2)^2 + (y1-y2)^2 + z1-z2)^2The minimization problem is constrained by the requirement that the points are on the ellipsoids.
Create the System of Equations for Use with fsolve
Finding the minimum distance using fsolve is done with the method of Lagrange Multipliers. This method transforms the constrained minimization problem into a system of nonlinear equations.
The details are beyond this tutorial, but the basic idea is that the solution points have the property that the vector between them is parallel to both normal vectors on the ellipsoids at the points. The system of equations enforces the parallel conditions and the requirement that the points be on the ellipsoids. The result is a system of eight equations.
- Start Compose.
-
From the File menu, select Open and locate the file
fsolveDemo.oml in
the<installation_dir>/tutorials/ folder. The file
contains code for the system of equations.

The function is called Residuals because it computes the residual errors in the system for a pair of candidate solution points.
Define Initial Values and Solve Using fsolve
The fsolve function requires an initial estimate of the solution. For this problem, most estimates are adequate, but we choose points near the centers of the ellipsoids for convenience. (Choosing the actual centers would create too many zero values in Residuals.)

The points and the distance between them are as follows:

Create the Objective and Constraint Functions to Use with fmincon
The Lagrange method used with fsolve is implemented internally in fmincon, so the set up with fmincon is different. Write the objective and constraint functions explicitly, as shown below.
- Start Compose.
-
From the File menu, select Open and locate the file
fminconDemo.oml in the
<installation_dir>/tutorials/ folder. The file
contains code for the objective and constraint functions.

fmincon handles both equality and inequality non-linear constraints. Inequality constraints would be stored as the variable c in ConFunc(), but since there are none, c is an empty matrix.
Define Initial Values and Solve Using fmincon
fmincon requires an initial estimate, just as fsolve did. It also supports bounds on the design variables. The code looks like this:

If the constraints in this problem had been linear, a ConFunc() function would not be needed. Instead, linear inequality constraints would be passed to fmincon as matrices in arguments 3 and 4, and linear equality constraints would be passed in arguments 5 and 6.
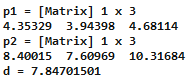
The points and the distance between them are as follows:
Create the Objective and Constraint Functions to Use with ga
ga is a genetic algorithm. It does not use derivatives and so it is inefficient for the problem in this demo compared to the other methods.
- Start Compose.
-
From the File menu, select Open and locate the file
gaDemo.oml in the
<installation_dir>/tutorials/ folder. The file contains code
for the objective and constraint functions.

This is similar to what was used with fmincon. It is difficult for ga to follow a contour, so you can use an inequality constraint instead because the solution is on the boundary. This gives the ga algorithm more freedom to find paths to the solution.
Define Initial Values and Solve Using ga

Trial and error shows that increasing the population size beyond the default produces a better result for this problem.

ga should not be expected to produce high precision results. It is best reserved for problems for which derivative based methods cannot be applied.
Create the Objective Function to Use with fminunc
To solve the problem with fminunc, it must be transformed into an unconstrained problem. To do this, you must re-parameterize the objective function in terms of the constraints so that a separate description of the constraint is no longer needed. This cannot be done in general.
- Start Compose.
-
From the File menu, select Open and locate the file
fminuncDemo.oml in the
<installation_dir>/tutorials/ folder. The file contains code
for the objective function.
An ellipsoid, using the standard notation, can be parameterized with two angles as follows:
x = a*cos(theta) + x0; y = b*sin(theta)*cos(phi) + y0; z = c*sin(theta)*sin(phi) + z0;There will be two angles for each ellipsoid, as shown in the code below:

Define Initial Values and Solve Using fminunc
fminunc requires an initial estimate for the angles. For this problem, most estimates are adequate, except zeros. The code looks like this:

The points and the distance between them are as follows:
