SS-V：6000 単純支持された正方形薄板 - 調和強制振動応答

テスト番号VD01 調和強制振動を受ける単純支持された正方形板の非定常応答を表示します。

定義

単純支持された正方形薄板（10 x 10 x 0.05 m）が、次の関数のように時間変動する均一な圧力P=100 Paを受けます。

P = 100 ∗ sin ( ω ∗ t ) MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake aacaWGqbGaeyypa0JaaGymaiaaicdacaaIWaGaey4fIOIaci4Caiaa cMgacaGGUbWaaeWaaeaacqaHjpWDcqGHxiIkcaWG0baacaGLOaGaay zkaaaaaa@45C6@

ここで、
ω = 2 ∗ P I ∗ f MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake aacqaHjpWDcqGH9aqpcaaIYaGaey4fIOIaamiuaiaadMeacqGHxiIk caWGMbaaaa@40B2@
f MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake aacaWGMbaaaa@39A2@
励振振動数。

励振振動数は、0から板の最初の共振振動数のすぐ上までの範囲で変化します。

動解析の解を近似するために16個のモードが使用され、すべてのモードで2%のモーダル減衰が仮定されます。

材料特性は以下の通りです：
特性
値
弾性係数
2.e+11 Pa
ポアソン比
0.3
密度
8.e+3 kg/m3

結果

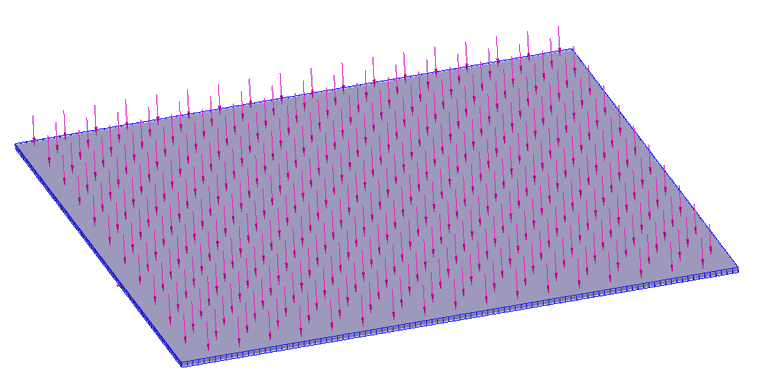
板は3Dソリッドボディとしてシミュレートされます。ヒンジ拘束を適用するために、板の中心面でスポットラインが作成されました（図 1）。
Figure 1.


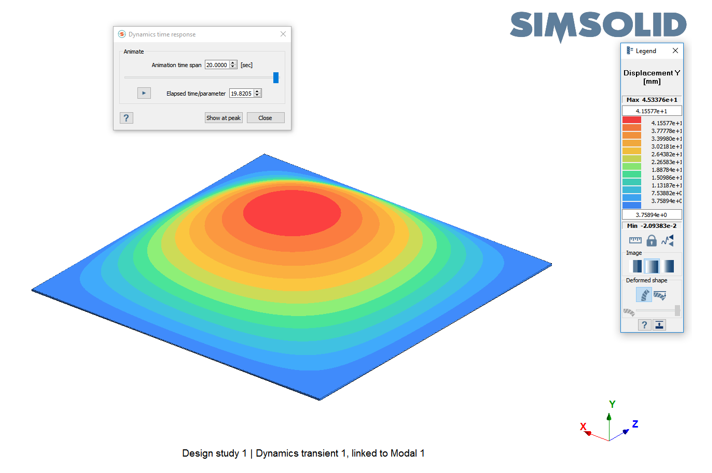
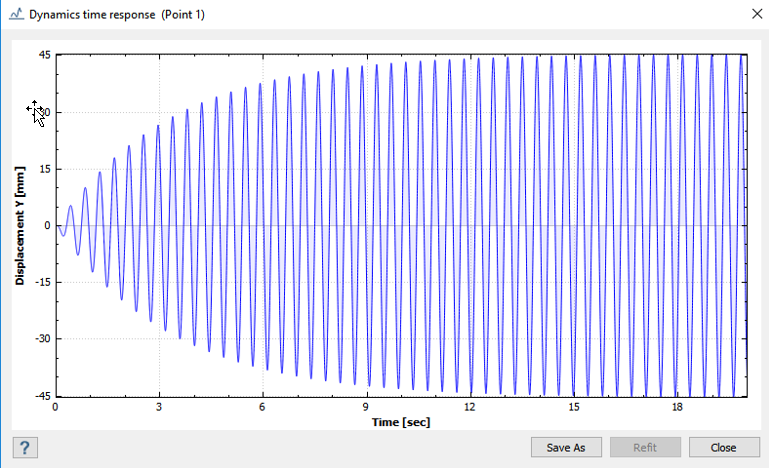
励振振動数が板の最初の固有振動数に等しくなると、ピーク応答に達します。これは励振の開始から19.82秒後に発生します。
Figure 2.


次の表は、ピーク応答の比較を示しています。
たわみY、mm 表面応力、MPa
45.34 31.86 SimSolid、ソリッドモデル
45.42 35.08 基準、薄板モデル
Figure 3. 応答の非定常と定常の部分


1 Test 13H from NAFEMS Publication R0016, “Selected Benchmarks for Forced Vibration” J. Maguire, D.J.Dawswell, L. Gould