/MAT/LAW71

Block Format Keyword This law describes the behavior of superelastic materials. It allows modeling the behavior of the shape memory alloys (such as Nitinol).

The particularity of these materials is that all of the strain is recovered upon unloading even when large deformations are reached. Besides, the material shows a hysteretic response in a complete loading-unloading cycle. The full recovery is due to phase change in the microstructure. The model is based on the work of Auricchio et al. 1997. This law is compatible with beam (/PROP/TYPE18 (INT_BEAM) only), solid and shell elements.

Format

(1)	(3)	(5)	(7)	(9)
/MAT/LAW71/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$υ$	`E_mart`
$σ_{S}^{A S}$	$σ_{F}^{A S}$	$σ_{S}^{S A}$	$σ_{F}^{S A}$	$α$
`EpsL`	`CAS`	`CSA`	`TS_AS`	`TF_AS`
`TS_SA`	`TF_SA`	`C`_p	`T`_ini

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`	Young's modulus. (Real)	$[Pa]$
$υ$	Poisson's ratio. (Real)
`E_mart`	Martensite Young's modulus. Default = 0.0 (Real)	$[Pa]$
$σ_{S}^{A S}$	Material parameter defining the start of phase transformation from austenite to martensite (AS). 1 (Real)	$[Pa]$
$σ_{F}^{A S}$	Material parameter defining the end of phase transformation from austenite to martensite (AS). 1 (Real)	$[Pa]$
$σ_{S}^{S A}$	Material parameter defining the start of phase transformation from martensite to austenite (SA). 1 (Real)	$[Pa]$
$σ_{F}^{S A}$	Material parameter defining the end of phase transformation from martensite to austenite (SA). 1 (Real)	$[Pa]$
$α$	Material parameter measuring the difference in response between tension and compression. Default = 0 (Real)
`EpsL`	Maximum residual strain. 2 (Real)
`CAS`	Stress-Temperature rate during loading. Default = 0 (Real)	$[\frac{Pa}{K}]$
`CSA`	Stress-Temperature rate during unloading. Default = 0 (Real)	$[\frac{Pa}{K}]$
`TS_AS`	Reference temperature for start of transformation (AS). Default = 298K (Real)	$[K]$
`TF_AS`	Reference temperature for end of transformation (AS). Default = 298K (Real)	$[K]$
`TS_SA`	Reference temperature for start of transformation (SA). Default = 298K (Real)	$[K]$
`TF_SA`	Reference temperature for end of transformation (SA). Default = 298K (Real)	$[K]$
`C`_p	Specific heat capacity. Default = 10³⁰ (Real)	$[\frac{J}{kg \cdot K}]$
`T`_ini	Initial temperature. Default = 360 K (Real)	$[K]$

Example (Metal)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW71/1/1
metal
#              RHO_I
             6.50E-9
#                  E                  Nu              E_mart
               62500                  .3               51000
#           sig_AS_s            sig_AS_f            sig_SA_s            sig_SA_f              alpha
                 450                 600                 300                 200                0.20
#               EpsL                 CAS                 CSA               TS_AS               TF_AS
               0.045                   1                   1                 383                 343
#              TS_SA               TF_SA                  CP                TINI
                 363                 403                 837                 360
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

If E_mart=0, then Young's modulus is considered constant, equal to E, and not dependent on the phase fraction of the material.
The different stresses $σ_{S}^{A S}$ , $σ_{F}^{A S}$ , $σ_{S}^{S A}$ and $σ_{F}^{S A}$ , defining the start and the end of phase transformation, as well as the residual strain EpsL, correspond to the case of a uniaxial tensile test:

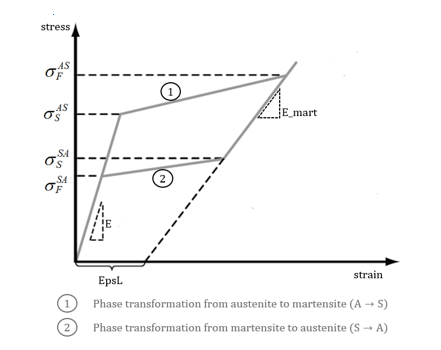
Figure 1.
The parameter $α$ is computed from the initial value of the austenite to martensite phase transformation in tension ${(σ_{S}^{A S})}_{T}$ and compression ${(σ_{S}^{A S})}_{C}$ from the relation.(1)
$α = \sqrt{\frac{2}{3}} \frac{{(σ_{S}^{A S})}_{C} - {(σ_{S}^{A S})}_{T}}{{(σ_{S}^{A S})}_{C} + {(σ_{S}^{A S})}_{T}}$

When /MAT/LAW71 is used with beam elements, the parameter must be set to $α = 1 - \sqrt{\frac{2}{3}}$ .

The Drucker-Prager type loading function

F

is introduced using the stress deviator

s

, the pressure

p

and the temperature.(2)

F = ‖ s ‖ + 3 α p

Two functions are defined for the start and the final point of transformation from austenite to martensite (A → S) or from martensite to austenite (S → A).

	(A→S)	(S →A)
Start point of transformation	$F_{S}^{A S} = F - R_{S}^{A S}$ $R_{S}^{A S} = σ_{S}^{A S} (\sqrt{\frac{2}{3}} + α) - C^{A S} (T - T_{S}^{A S})$	$F_{S}^{S A} = F - R_{S}^{S A}$ $R_{S}^{S A} = σ_{S}^{S A} (\sqrt{\frac{2}{3}} + α) - C^{S A} (T - T_{S}^{S A})$
Final point of transformation	$F_{F}^{A S} = F - R_{F}^{A S}$ $R_{F}^{A S} = σ_{F}^{A S} (\sqrt{\frac{2}{3}} + α) - C^{A S} (T - T_{F}^{A S})$	$F_{F}^{S A} = F - R_{F}^{S A}$ $R_{F}^{S A} = σ_{F}^{S A} (\sqrt{\frac{2}{3}} + α) - C^{S A} (T - T_{F}^{S A})$
Condition	$F_{S}^{A S} > 0$ $F_{F}^{A S} < 0$ $\dot{F} > 0$	$F_{S}^{S A} < 0$ $F_{F}^{S A} > 0$ $\dot{F} < 0$
Evolution equation of martensite	During loading: ${\dot{X}}_{m} = (1 - X_{m}) \frac{\dot{F}}{F - R_{F}^{A S}}$	During unloading: ${\dot{X}}_{m} = X_{m} \frac{\dot{F}}{F - R_{F}^{S A}}$

$σ_{S}^{A S}, σ_{F}^{A S}, T_{S}^{A S}, T_{F}^{A S}, α, C^{A S}, σ_{S}^{S A}, σ_{F}^{S A}, T_{S}^{S A}, T_{F}^{S A}, C^{S A}$ are the material parameters. The conversion of austenite to martensite takes place when above conditions (in table) are verified.

List of Animation output (/ANIM/BRICK/USRI):
- USR 1= Martensite phase fraction
- USR 2= Loading function
- USR 3= Unloading function