/MAT/LAW75 (POROUS)
Block Format Keyword Describes the P- porous material model. This material describes ductile Porous material with Herrmann model. It only works with 8-node brick element and is not compatible with ALE.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW75/mat_ID/unit_ID or /MAT/POROUS/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| mat_IDs | Iflag1 | Iflag2 | itemax | ||||||
| PE | Ps | n | |||||||
| tol | |||||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| mat_title | Material title (Character, maximum 100 characters) |
|
| Initial density for porous
material (Real) |
||
| E | Young's modulus (Real) |
|
| Poisson's ratio (Real) |
||
| mat_IDs | Material identifier of the solid (fully
compacted) material. (Integer) |
|
| Iflag1 | Pressure formulation flag.
(Integer) |
|
| Iflag2 | Deviatoric stresses formulation flag.
(Integer) |
|
| itemax | Maximum number of iterations on a
calculation. Default = 5 (Integer) |
|
| PE | Elastic compact pressure (elastic
limit). 3 (Real) |
|
| Ps | Solid (matrix) compact pressure. 3 (Real) |
|
| n | Exponent used for fitting the experiment
data. 3 Default = 2 (Real) |
|
| tol | Convergence tolerance on a calculation.
Default = 10-8 (Real) |
Example (Porous Soil)
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. LOCAL_UNIT_SYSTEm:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
g cm mus
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW75/1/1
porous soil
# RHO_I
1.7
# E NU
3 .3
# MAT_IDs IFLAG1 IFLAG2 ITEMAX
2 1 2 0
# PE PS N
.01 .05 0
# TOL
0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HYD_JCOOK/2/1
soil
# RHO_I RHO_O
1.76000004 0
# E nu
3.5999999 .300000012
# A B n epsmax sigmax
10000 0 0 0 0
# Pmin
0
# C EPS_DOT_0 M Tmelt Tmax
0 0 0 0 0
# RHOCP Troom
0 0
/EOS/POLYNOMIAL/2/1
EOS for soil
# C0 C1 C2 C3
0 2.81999993 2 -1.37
# C4 C5 E0 Psh RHO_0
1.53999996 1.53999996 0 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- The porosity
is defined as:
(1) Note that ≥ 1 ( )
Where,- Density of the solid (full compacted matrix) material
- Density of the porous material
- If the EOS of the solid (matrix)
material is:
(2) Then the EOS of the porous material is:- for Herrmann formulation
- for modified Herrmann formulation
Where, ( ) is the internal energy per unit mass. It is same in porous material and in the solid (matrix) material.
- If
the behavior is elastic, and if
describes plastic region.
In the elastic region, the change of porosity with pressure is reversible.
In the plastic region, the porosity is assumed to depend on pressure as described below:(3) Where,- Porosity where pressure reach the elastic compact pressure
- Pressure reaches the solid (matrix) compact pressure
- Iinitial porosity
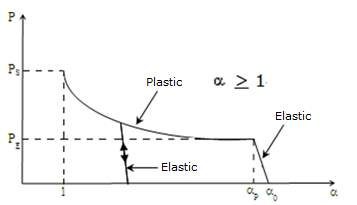
Figure 1.