/MAT/LAW169 (ARUP_ADHESIVE)

Block Format Keyword This is an elastoplastic connection material law with coupled damage and failure. It can be used to model adhesives.

The yield and failure surfaces are described through a power law combination of normal and shear stresses. This material is applicable only to solid hexahedron elements (/BRICK) and connection property (/PROP/TYPE43 (CONNECT)).

Format


(1)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW169/`mat_ID`/`unit_ID` or /MAT/ARUP_ADHESIVE/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$ν$	`SHT_SL`		`TENMAX`	`GCTEN`
`SHRMAX`	`GCSHR`	`PWRT`	`PWRS`	`SHRP`

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit identifier. (Integer, maximum 10 digits
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`	Young’s (stiffness) modulus per unit length in tension. 1 (Real)	$[\frac{P a}{m}]$
$ν$	Poisson ratio. Default = 0.0 (Real)
`SHT_SL`	Slope of yield surface at zero normal stress. 3 Default = 0.0 (Real)
`TENMAX`	Maximum stress in normal direction. Default = 1²⁰(Real)	$[Pa]$
`GCTEN`	Energy per unit area to fail in normal direction. 5 6 Default = 1²⁰(Real)	$[\frac{J}{m^{2}}]$
`SHRMAX`	Maximum stress in shear direction. Default = 1²⁰ (Real)	$[Pa]$
`GCSHR`	Energy per unit area to fail in shear direction. 5 6 Default = 1²⁰ (Real)	$[\frac{J}{m^{2}}]$
`PWRT`	Power law exponent for normal direction. Default = 2 (Integer)
`PWRS`	Power law exponent for shear direction. Default = 2 (Integer)
`SHRP`	Shear plateau ratio. Default = 0.0 (Real)

Example

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1 
unit for mat
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW169/1/1
ARUP MATERIAL
#              RHO_I
              7.8E-6
#                  E                  PR              SHT_SL              TENMAX               GCTEN
                1.89                 0.3                   2                 1.6                 2.0
#             SHRMAX               GCSHR      PWRT      PWRS                SHRP             
                 0.8                 1.2         2         2                   0                   
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

The Young's modulus is defined per displacement in order to be independent from the initial height of the solid element.
For example, E=210000 MPa/mm means that the normal stress increases by 210000 MPa for each 1 mm of displacement until the yield stress limit or the failure limit are reached.
The shear stiffness is computed using the Young's modulus and Poisson ratio.
$G = \frac{E}{2 (1 + ν)}$
The yield and failure surfaces are described by a power law using the normal and shear stresses.
${(\frac{\max (0, σ_{Z Z})}{T E N M A X})}^{P W R T} + {(\frac{τ}{S H R M A X - S H T_S L \cdot σ_{Z Z}})}^{P W R S} = 1$
Where, $τ = \sqrt{σ_{y z}^{2} + σ_{x z}^{2}}$
The plasticity model is not volume conserving. The plasticity only occurs in shear.
The two parameters GCTEN and GCSHR are respectively the areas under the curves of stress versus displacement for pure tension and pure shear.
Figure 1. Stress- displacement curves for pure tension and pure shear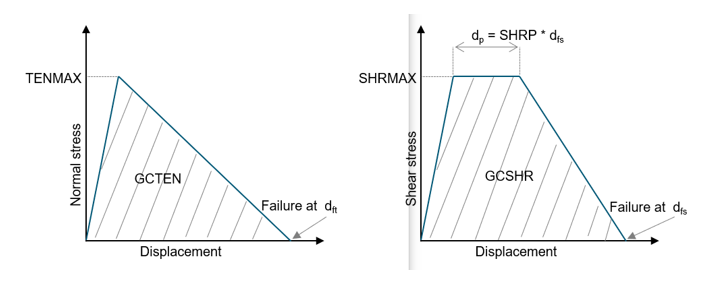
The failure displacement limits are defined with:
- In pure tension
  $d_{f t} = \frac{2 \cdot G C T E N}{T E N M A X}$
- In pure shear
  $d_{f s} = \frac{2 \cdot G C S H R}{(1 + S H R P) \cdot S H R M A X}$
Element is deleted when one failure limit is reached.
Energy per unit area to fail will be updated in the Starter to respect the following conditions.
- $G C T E N \geq \frac{T E N M A X^{2}}{2 E}$
- $G C S H R \geq \frac{S H R M A X^{2}}{2 G} + S H R M A X \cdot d_{p}$
All nodes of the solid elements must be connected to other shells or solid elements, secondary nodes of rigid body (/RBODY) or secondary nodes of tied interface (/INTER/TYPE2).