OS-V: 0460 Dynamic Behavior of a Fluid-containing Structure using MFLUID
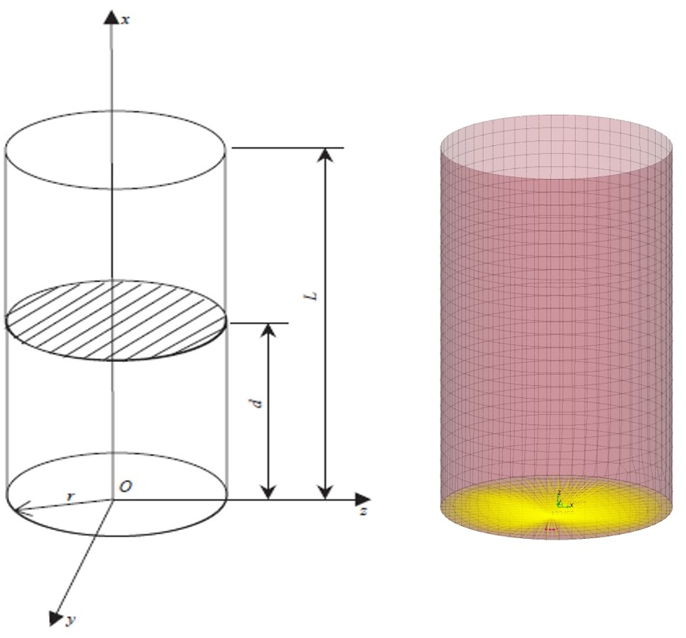
A vertical clamped free cylindrical shell with a rigid bottom is chosen to demonstrate the applicability of the structures which are partially filled such as liquid storage tanks.
Model Files
Benchmark Model
In a preliminary calculation the natural frequencies and principal mode shapes of the dry structure (empty tank) are determined. In these calculations, the cylindrical shell is discretized with 8-noded quadrilateral shell elements, including both membrane and bending stiffness influences.
- The fluid is inviscid and incompressible. The fluid flow is a potential flow.
- The fluid is nearly incompressible, the structural modes are below the compressible fluid modes.
- There is no gravity effect or sloshing effect.
There is no acoustic effect involved. The modes from the structural side do not couple with the modes of the nearly incompressible fluid modes.
MFLUID is used to mimic the mass effect of an incompressible inviscid fluid in contact with a structure. It does not represent the actual mass of the fluid. There is no mesh needed for the fluid domain. The Virtual Fluid Mass represents the full coupling between acceleration and pressure at the fluid-structure interface. A dense mass matrix is generated among damp grids at the fluid-structure interface.
- Cylindrical Shell
- Length (L)
- 231 mm
- Radius (r)
- 77:25 mm
- Thickness (t)
- 1.5 mm
- Plate (2D) Elements and Rigid
- Cylinder Tank
- CQUAD8
- Cylinder Bottom
- RBE2
- Cylinder: Linear Material - MAT1
- Young’s Modulus
- 205000
- Poisson's Ratio
- 0.3
- Initial Density
- 7.8E-9
- Fluid (Water) Inside the Tank (using MFLUID)
- Density
- 1000 kg/m3
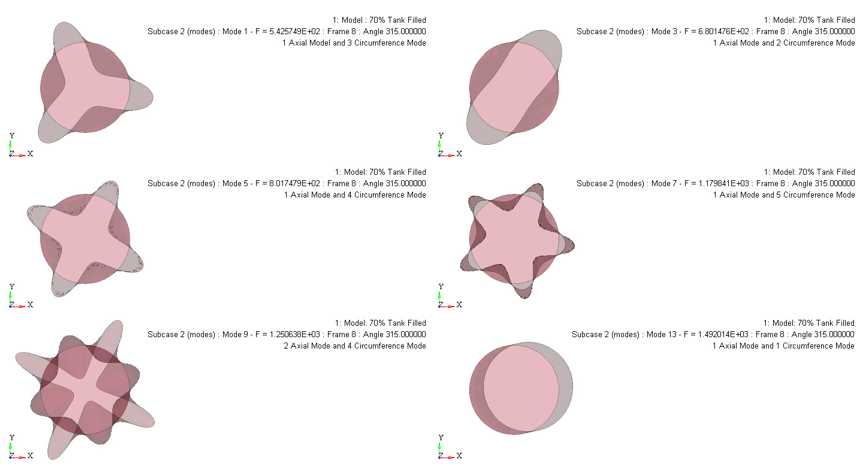
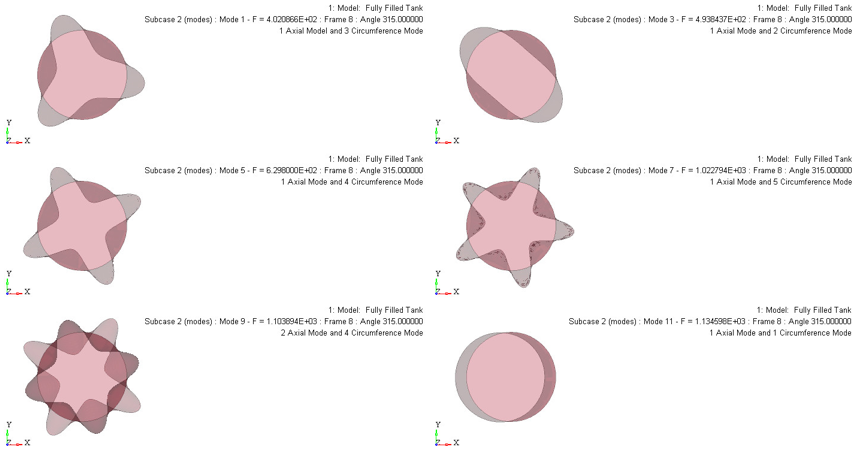
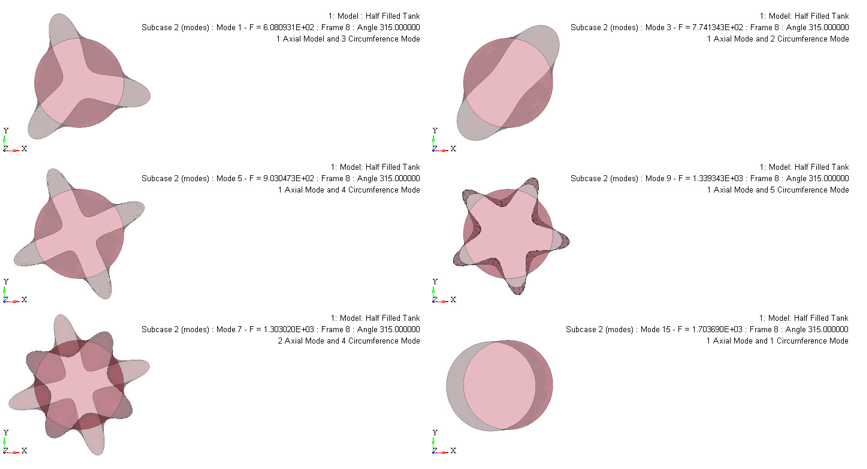
Results
| Mode Type | Half Filled Tank | 70% Filled Tank | Fully Filled Tank | |||
|---|---|---|---|---|---|---|
| Experimental | OptiStruct | Experimental | OptiStruct | Experimental | OptiStruct | |
| 1 Axial 3 Circumference |
609.4 | 608.0 | 552 | 542.5 | 388 | 402.0 |
| 1 Axial 2 Circumference |
771.1 | 774.1 | 582 | 680.1 | 421 | 493.8 |
| 1 Axial 4 Circumference |
908.8 | 903.0 | 789 | 801.7 | 628 | 629.8 |
| 1 Axial 5 Circumference |
1352.8 | 1339.3 | 1196 | 1179.8 | 1027 | 1022.7 |
| 2 Axial 4 Circumference |
1303.9 | 1303.0 | 1244 | 1250.6 | 1094 | 1103.8 |
| 1 Axial 1 Circumference |
1654.4 | 1703.6 | N/A | 1492.0 | N/A | 1134.5 |
Reference
Mazuch T., "Natural modes and frequencies of a thin clamped–free steel cylindrical storage tank partially filled with water: FEM and Measurements, Journal of Sound and Vibration" 193, (1996) 669–69