HS-3010: Fuselage Sizing Trade-Off using Categorical Variables
Learn how to create a Fit in order to investigate the relative effect of the variable on the identified output responses, and identify a combinations of variables that were not explicitly simulated.
- Continuous variables
- Thickness of floor
- Thickness of floor beams
- Skin thickness
- Category variables
- Cross sections of the frames
- Stringers above the floor
- Stringers below the floor
- Load cases
- Free-free normal modes case
- Simple bending case
- Simple torsional case
Figure 1.
Perform the Study Setup
-
Start a new study in the following ways:
- From the menu bar, click File > New.
- On the ribbon, click
 .
.
- In the Add Study dialog, enter a study name, select a location for the study, and click OK.
- Go to the Define Models step.
-
Add a Parameterized File model.
-
From the Directory, drag-and-drop the fuselage.tpl
file into the work area.
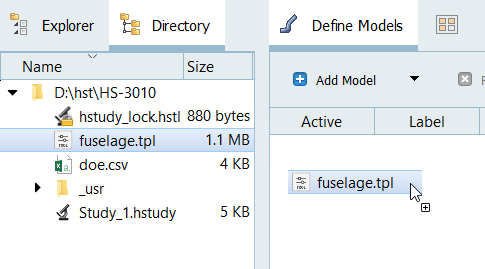
Figure 2. -
In the Solver input file column, enter
fuselage.fem.
This is the name of the solver input file HyperStudy writes during any evaluation.
- In the Solver execution script column, select Optistruct (os).
-
From the Directory, drag-and-drop the fuselage.tpl
file into the work area.
-
Click Import Variables.
Six input variables are imported from the fuselage.tpl resource file.
- Go to the Define Input Variables step.
- Review the input variable's lower and upper bound ranges.
-
Modify input variable mode.
- Click the Modes tab.
-
In the Mode column, change the input variables defined as Discrete to
Categorical.
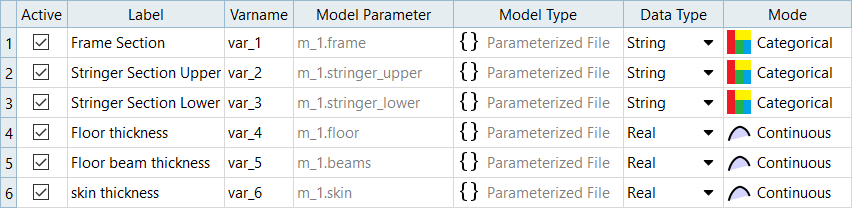
Figure 3.
Perform Nominal Run
- Go to the Test Models step.
-
Click Run Definition.
An approaches/setup_1-def/ directory is created inside the study directory. The approaches/setup_1-def/run__00001/m_1 directory contains the input file, which is the result of the nominal run.
Create and Evaluate Output Responses
- Go to the Define Output Responses step.
-
Create the Mass output response.
- From the Directory, drag-and-drop the fuselage.out file, located in approaches/setup_1-def/run__00001/m_1, into the work area.
- In the File Assistant dialog, set the Reading technology to Altair® HyperWorks® and click Next.
- Select Single item in a time series and click Next.
-
Define the following options:
- Type: Mass
- Request: Mass
- Component: Value
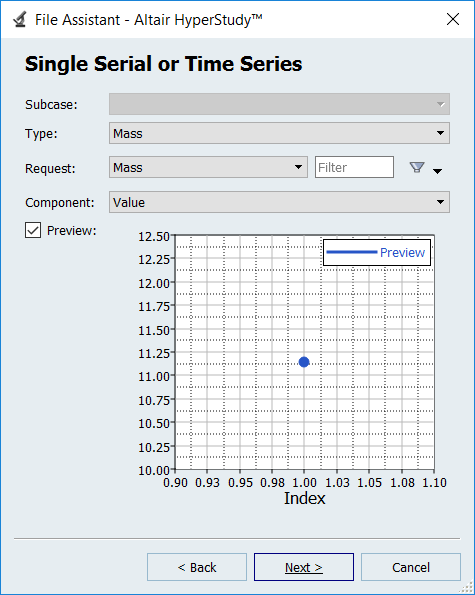
Figure 4. - Click Next.
- Label the output response Mass.
- Set Expression to Maximum.
-
Click Finish.
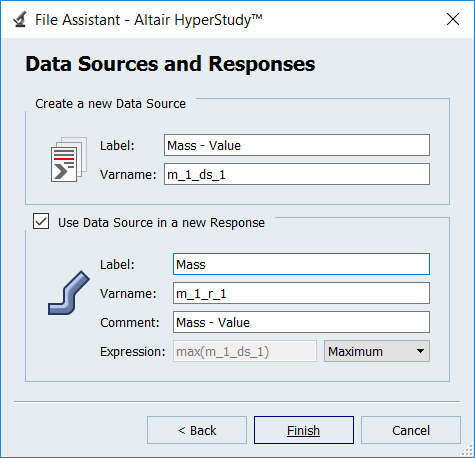
Figure 5.
-
Using step 2
create two more output responses substituting the Type, Request, and Component
for those shown in Table 1.
Because this is a free-free analysis, Freq1 will be the seventh frequency in the list due to the six rigid body modes (all near zero). Freq2 will be the eighth frequency in the list.
Table 1. Output Response Type Request Component Freq1 Frequency Mode 7 Value Freq2 Frequency Mode 8 Value -
Create the Bending displacement output response, which will have a magnitude of
node 8196 (loading point).
- From the Directory, drag-and-drop the fuselage.h3d file, located in approaches/setup_1-def/run__00001/m_1, into the work area.
- In the File Assistant dialog, set the Reading technology to Altair® HyperWorks® and click Next.
- Select Single item in a time series, then click Next.
-
Define the following options and click
Next.
- Subcase: Subcase 2 (bending)
- Type: Displacement (Grids)
- Request: Apply a Filter of 8196
- Component: MAG
- Label the output response Bending displacement.
- Set Expression to Maximum.
- Click Finish.
-
Create the Torsional rotation output response, which will have a z-direction of
node 8196 (loading point).
- From the Directory, drag-and-drop the fuselage.h3d file, located in approaches/setup_1-def/run__00001/m_1, into the work area.
- In the File Assistant dialog, set the Reading technology to Altair® HyperWorks® and click Next.
- Select Single item in a time series, then click Next.
-
Define the following options and click
Next.
- Subcase: Subcase 3 (torison)
- Type: Rotation (Grids)
- Request: Apply a Filter of 8196
- Component: Z
- Label the output response Torisonal rotation.
- Set Expression to Maximum.
- Click Finish.
-
In the Expression field for Torsional rotation, edit the expression to
be max(m_1_ds_5)*180/3.14.
This expression converts the rotation from radians to degrees.
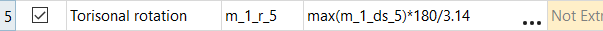
Figure 6.
- Click Evaluate to extract the response values.
- Click OK.
Run DOE
-
Add a DOE.
-
In the Explorer, right-click and select
Add from the context menu.
The Add dialog opens.
- For Definition from, select an approach.
- Select DOE and click OK.
-
In the Explorer, right-click and select
Add from the context menu.
- Go to the DOE 1 > Specifications step.
- In the work area, set the Mode to None.
- Click Apply.
-
Edit run matrix.
-
In the top, right of the work area, select Edit > Run Matrix.

Figure 7. - In the Edit Run Matrix dialog, remove any existing run data.
- Click Import Values.
- In the Import Values dialog, select Plain Text and click Next.
- In the Source File field, navigate to the doe.csv file.
- Click Next.
- Click Finish.
-
Review the imported run data and click Apply.
Figure 8. - Click OK.
-
In the top, right of the work area, select Edit > Run Matrix.
- Go to the DOE 1 > Evaluate step.
- Click Evaluate Tasks.
- Go to the DOE 1 > Post-Processing step.
-
Review Pareto plot.
- Click the Pareto Plot tab.
-
Click
 (Multiplot).
(Multiplot).
-
Select all of the output responses in the Channel selector.
If not all of the input variables are plotted, you may need to alter the number of displayed input variables from the options menu.
The relative effect of a input variable can vary from output response to output response. The most influential input variables when analyzing frequency output responses are Frame Section and Stringer Section Upper. In contrast, the most influential input variables when analyzing the two stiffness conditions are Skin thickness and Stringer Section Upper.
Some input variables can have no effect on output responses. Floor beam thickness has minimal effect on any of the output responses, which indicates that you may want to consider removing this input variable from the analysis.
In a Pareto plot, the effect of input variables on output responses does not measure sensitivity but rather absolute change. Floor thickness has a major effect on Volume. This effect is not a derivative, but a measure of the possible increase over the range of the input variables (the range is the difference between the upper and lower bounds). The floor has a large area and the thickness has very large bounds (+/-0.1 inches), therefore it can make a dramatic impact on Volume as the input variables move through the available space.
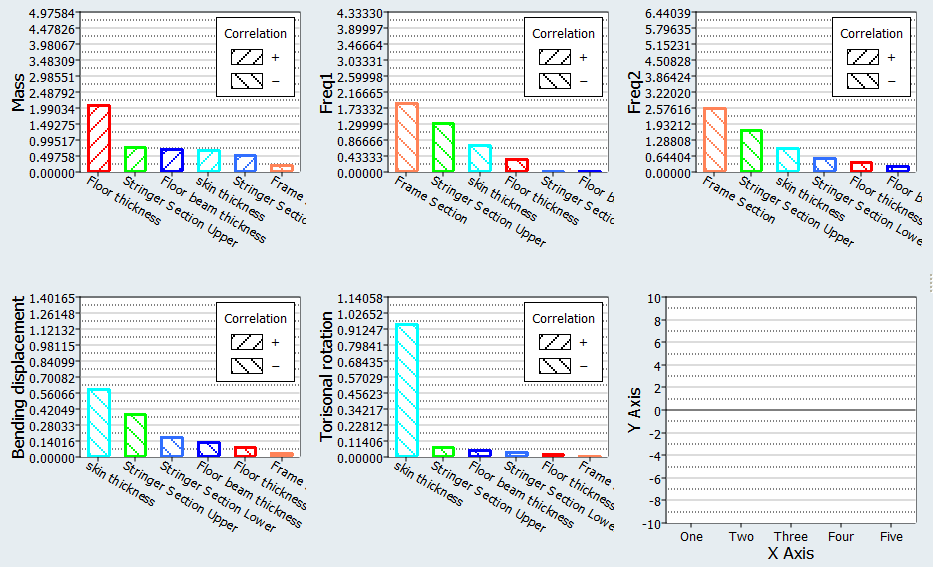
Figure 9.
Run Least Squares Regression Fit
-
Add a Fit.
- In the Explorer, right-click and select Add from the context menu.
- In the Add dialog, select Fit and click OK.
-
Import matrix.
- Go to the Fit 1 > Specifications step.
- Click Add Matrix.
- In the work area, set Matrix Source to Doe 1 (doe_1).
- Click Apply.
-
Define specifications.
- In the work area, Fit Type column, select Least Squares Regression for all output responses.
- Click Apply.
Figure 10. -
Evaluate tasks.
- Go to the Fit 1 > Evaluate step.
- Click Evaluate Tasks.
- Go to the Fit 1 > Post-Processing step.
-
Assess the accuracy of the Fit.
- Click the Diagnostics tab.
-
Select the Mass output response.
The R-Square and R-Squared Adjusted values for Mass are close to 1.00, which indicates the model almost perfectly predicted the known values.
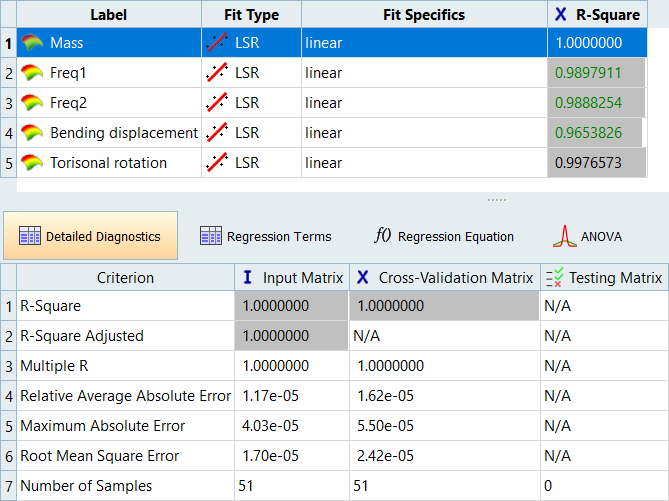
Figure 11. - Review the diagnostics for the remaining output responses. Notice the R-Squared values are still high, which indicates a high quality fitting of the data.
-
Click the ANOVA tab and review the Mean
Squares Percent column to see the relative importance of input
variables.
The results should be similar to the results noted in the Pareto Chart tab of the Doe.
- Click the Trade-Off tab to perform "what if" scenarios. In the Inputs pane, modify the values of input variables to see their effect on the output response approximations in the Output pane.