Laminar Couette Flow with Imposed Pressure Gradient and Heated Walls
In this application, AcuSolve is used to simulate the flow of a highly viscous fluid between a moving and a stationary plate with an imposed pressure gradient and fixed temperature on the walls. AcuSolve results are compared with analytical results described in White (1991). The close agreement of AcuSolve results with analytical results validates the ability of AcuSolve to model cases with imposed pressure gradients and viscous heating.
Problem Description
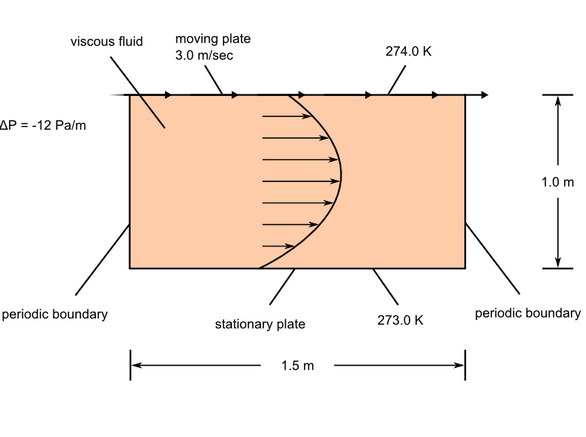

AcuSolve Results

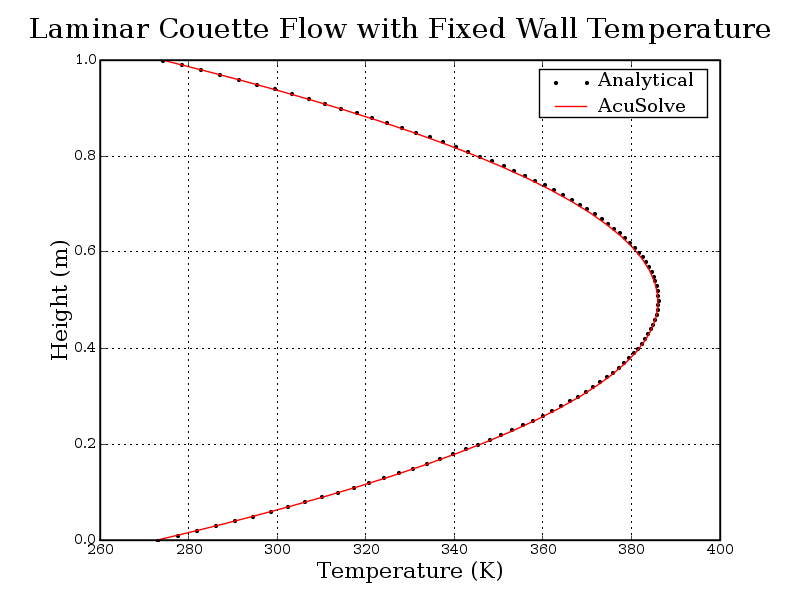
Summary
In this application, a fully developed laminar flow between two plates with fixed temperature is studied and compared against analytical data. The AcuSolve results compare well with the analytical data for the temperature distribution between the two plates. The simulation indicates that the velocity profile arises due to the combination of the viscous shearing and the velocity of the upper plate. The velocity and temperature profiles computed by AcuSolve demonstrate how highly viscous fluids tend to direct the flow regime. AcuSolve demonstrates the ability to predict the analytical solution for viscous heating between two flat plates with moving and stationary boundaries and an imposed pressure gradient.
Simulation Settings for Laminar Couette Flow with Imposed Pressure Gradient and Heated Walls
SimLab database file: <your working directory>\couette_laminar_heat\couette_laminar_heat.slb
Global
- Problem Description
- Flow - Steady State
- Temperature equation - Advective Diffusive
- Turbulence equation - Laminar
- Auto Solution Strategy
- Relaxation factor - 0.2
- Material Model
- Fluid
- Density - 1.0 kg/m3
- Specific Heat - 1.0 J/kg-K
- Viscosity - 100.0 kg/m-sec
- Fluid
- Body Force
- DP/DL
- Gravity
- Z-component - 18.0 m/sec2
- Gravity
Model
- DP/DL
- Volumes
- Fluid
- Element set
- Material model - Fluid
- Body force - DP/DL
- Viscous heating - on
- Element set
- Fluid
- Surfaces
- Max_X
- Simple Boundary Condition
- Type - Symmetry
- Simple Boundary Condition
- Max_Y
- Simple Boundary Condition
- Type - Wall
- Wall velocity type - Cartesian
- Z-velocity - 3.0 m/s
- Temperature - 274.0 K
- Simple Boundary Condition
- Max_Z
- Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
- Min_X
- Simple Boundary Condition
- Type - Symmetry
- Simple Boundary Condition
- Min_Y
- Simple Boundary Condition
- Type - Wall
- Temperature - 273.0 K
- Simple Boundary Condition
- Min_Z
- Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
- Max_X
- Periodics
- Periodic 1 all
- Periodic Boundary Conditions
- Type - Periodic
- Periodic Boundary Conditions
- Periodic 1 all
References
F. M. White. "Viscous Fluid Flow". Section 3-3.2. McGraw-Hill Book Co., Inc. New York. 1991.