Depuis la version 2026, Flux 3D et Flux PEEC ne sont plus disponibles.
Veuillez utiliser SimLab pour créer un nouveau projet 3D ou pour importer un projet Flux 3D existant.
Veuillez utiliser SimLab pour créer un nouveau projet PEEC (pas possible d'importer un projet Flux PEEC existant).
/!\ La documentation est en cours de mise à jour – des références au 3D peuvent subsister.
Grandeurs vectorielles
Introduction
Les grandeurs disponibles à l'exploitation peuvent être des grandeurs scalaires ou des grandeurs vectorielles.
Ce paragraphe traite des grandeurs vectorielles et rappelle quelques définitions : notation complexe, représentation elliptique…
Grandeurs vectorielles (notation complexe)
Pour une grandeur vectorielle, il est possible d'écrire que chacune des composantes est une grandeur sinusoïdale :
![]() ; …
; …
qui s'écrit en notation complexe :
![]() ; …
; …
![]() ; …
; …
où :
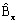 est le module de
la composante complexe
est le module de
la composante complexe 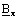
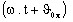 est l'argument (ou
la phase) de la composante complexe
est l'argument (ou
la phase) de la composante complexe 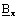
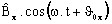 est la partie
réelle de la composante complexe
est la partie
réelle de la composante complexe 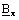
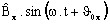 est la partie
imaginaire de la composante complexe
est la partie
imaginaire de la composante complexe 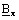
Représentation elliptique en 2D
Dans le cas général 2D, les grandeurs vectorielles se déplacent au cours du temps, sur des ellipses.
En chaque
point de l'espace, le champ d'induction magnétique ![]() peut s'écrire :
peut s'écrire :
![]()
![]()
Ce qui est l'équation paramétrique d'une ellipse.
-
où
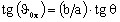
-
où
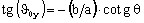
a est appelé “1/2 grand axe” et b est appelé “1/2 petit axe”