Grandeurs scalaires, notion de phaseur

Introduction

Les grandeurs disponibles à l'exploitation peuvent être des grandeurs scalaires ou des grandeurs vectorielles.

Ce paragraphe traite des grandeurs scalaires et rappelle quelques définitions : notation complexe, vecteur tournant, phaseur…

Représentation complexe

Une grandeur scalaire sinusoïdale, de pulsation ω, peut être représentée géométriquement par un vecteur tournant à la vitesse angulaire ω.

Ce vecteur est la représentation géométrique d'un nombre complexe.

Exemple : courant sinusoïdal

On s'intéresse à un courant sinusoïdal i : d'amplitude Î, de pulsation ω (ω =2 π f), de phase à l'origine β (à t = 0).

La valeur instantanée du courant sinusoïdal i : i = Î.sin(ω.t + β)

est égale à la partie imaginaire du nombre complexe i : i = Im( i )

Vecteur tournant à la vitesse ω	Grandeur sinusoïdale de période T= 2 π / ω

Ainsi la valeur instantanée complexe d'un courant sinusoïdal est donnée par la relation suivante :

• sous forme cartésienne : i = Î.cos(ω.t + β)+j.Î.sin(ω.t + β)
• sous forme exponentielle : i = Î.e j(ω.t + β)

où :

• Î est le module du nombre complexe i
• ω.t + β est l'argument (ou la phase) du nombre complexe i
• β est la phase à l'origine

Notation complexe

Le vecteur tournant associé une grandeur sinusoïdale s'exprime sous la forme d'un nombre complexe A.

Ce nombre complexe A peut s'écrire :

• sous forme cartésienne :
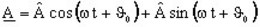
• sous forme exponentielle :

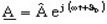
Notion de phaseur

Le nombre complexe A associé à la grandeur sinusoïdale A(t) peut se décomposer en deux termes :

Cette décomposition est présentée dans le tableau ci-dessous.

Le terme …	qui peut s'écrire …	correspond …
		au vecteur tournant associé à la grandeur A(t) à l'origine (t=0)
		à une rotation supplémentaire d'un angle ω.t

• Le terme 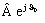contient les informations relatives à l'amplitude et la phase à l'origine de la grandeur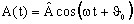

• Le terme e^jωt contient l'information sur la manière dont cette valeur varie avec le temps

Notion de phaseur

Une fonction sinusoïdale dans le monde temporel :

peut être représentée par un phaseur dans le monde des complexes

Phaseur : définition

On appelle le phaseur associé à la grandeur

ou si l'on préfère le phaseur associé à la grandeur est le vecteur tournant associé à cette grandeur pris au temps t = 0.