Formulation : généralités

Introduction

Ce paragraphe présente les notions de variable d'état, de formulation et de modèle de formulation.

Notion de variable d'état

D'un point de vue théorique, à chacune des applications physiques correspond un système d'équations.

Pour résoudre ce système d'équation on utilise des variables de calcul appelées variable d'état qui permettent alors de ramener le système d'équation à une ou deux équations. (On pourra alors recalculer toutes les grandeurs électromagnétiques à partir de ces variables).

Exemples :

• application électrique : la variable d'état est le potentiel électrique V
• application thermique : la variable d'état est la température T

Notion de formulation

Dans Flux, à chaque région est associée une formulation qui permet de dire :

• quelle est la variable d'état ?
• quelle est l'équation résolue et comment ?

Exemples :

• application électrostatique : (formulation ES3SCA)
  • la variable d'état est le potentiel électrique V (noté PHI1 dans Flux 3D)
  • l'équation résolue est l'équation suivante :

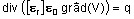
• application conduction électrique : (formulation EC3SCA)
  • la variable d'état est le potentiel électrique V (noté PHI1 dans Flux 3D)
  • l'équation résolue est l'équation suivante :

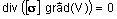
Formulation et applications

Pour les applications électriques et les applications thermiques, une seule méthode de résolution est proposée. Ce qui se traduit par une seule formulation Flux pour l'ensemble des régions du domaine (cf. exemples précédents).

Pour les applications magnétiques, différentes méthodes de résolution sont proposées. Ce qui se traduit par le choix d'une formulation Flux pour chacune régions du domaine (cf. bloc suivant).

Notion de modèle

Les différentes formulations proposées dans le cadre des applications magnétiques peuvent être regroupées et on parle alors d'un modèle de formulation.

Les deux modèles proposés dans le cadre des applications magnétiques sont :

• le modèle vecteur qui utilise :

  le potentiel vecteur magnétique A et le potentiel scalaire électrique V

• le modèle scalaire qui utilise :

  différents potentiels scalaires magnétiques ϕ et le potentiel vecteur électrique T