Optimising the Bandpass Filter with HyperStudy Using a POSTFEKO Session

Configure the bandpassfilter.pfs file with the S11 data to minimise the reflection coefficient in HyperStudy.

  1. Open CADFEKO.
  2. Click Application Macro under the Scripting group.
  3. In the drop-down list, select Macro Library and run the EG I3: Bandpass Filter script.
    Figure 1. The Application Macro Collection dialog.


  4. Save the model with the name bandpassfilter.cfx and execute the solver.
  5. Launch POSTFEKO from inside CADFEKO or open bandpassfilter.fek in POSTFEKO.
  6. Create a Cartesian graph and add the S11 trace from the SParamOpt request.
  7. [Optional] From the Measure tab add a Global minimum annotation to the graph to extract this value to a data source in HyperStudy.
    Note: Other annotations are also supported and will be extracted from a Cartesian or Polar graph.
    Figure 2. The reflection coefficient (S11) of the bandpass filter before optimisation from 3.960 GHz to 4 GHz.


  8. Save the bandpassfilter.pfs file in the same location as the bandpassfilter.cfx.
  9. On the Home tab in the in the Scripting group, click Application macro.
    The scripts loaded in the Macro library is displayed.
    Figure 3. Example of the scripts available Application macro library.


  10. Click Utility and select Optimise Model in HyperStudy.
    The following Create HyperStudy Session dialog is shown.
    Figure 4. The Create HyperStudy Session dialog.


  11. In the Study label field, enter a value for the name of the study.
  12. In the Study folder field, specify a value for the directory of the HyperStudy session.
  13. In the Installation directory field, specify the directory where HyperStudy is installed.
    Note: Use the following structure when pointing to the HyperStudy installation directory: <hw_installation_root>/hwdesktop/hst
  14. [Optional] Set the FEKO_HST_INSTALLATION_DIR environment variable to use a specific version of HyperStudy.
  15. [Optional]Select Create HyperStudy preference file to create a preference file with the correct solver path for the current installation.
  16. [Optional] Select Launch HyperStudy to launch HyperStudy after creating the HyperStudy session.
  17. Click OK to start to create a HyperStudy session.
    The following Create HyperStudy Session dialog is shown.


    The extraction script bandpassfilter.cfx_extract.lua is created in the same directory as the bandpassfilter.pfs.
    Note: The trace on the Cartesian graph is extracted to the HyperStudy output file automatically. No additional scripting is required in the bandpassfilter.cfx_extract.lua file.
  18. Click OK to launch HyperStudy.
  19. Under the File menu, select Use Preferences File and set the preference file in the study folder.
    Figure 5. An example of how to select a custom preference file.


  20. Under Define models, verify the Solver Execution Script field is set to use the correct solver version.
    Note:
    • The script is accessible under Edit > Register Solver Script, which offers the possibility to register another solver or version.
    • The argument -np can be typed in Solver Input Arguments to specify the number of cores to use.

    • If a legacy CADFEKO model is optimised the solver path should point to %FEKO_HOME%/bin/legacy/feko/bin/runfeko.bat
  21. Under Define Input Variables, select which variables to include in the study. Only S1 – S3 should be activated and the default ranges used.
    An example of the selected variables is displayed.
    Figure 6. Example of the variable selection


  22. Click Next.
  23. Click Run Definition.
    Figure 7. Example selecting the Run Definition button.


    During the Write phase, the bandpassfilter.cfx_extract.lua file was copied to the run directory and executed after the Feko solver was run in the Extract phase. This generated an output file that HyperStudy can process easily.
    Note: The script bandpassfilter.cfx_extract.lua is different if a .pfs file was present before importing the variables and will automatically extract the visible traces on a Cartesian graph and polar graph.
    See Figure 8 for the completed definition run for the Write, Execute and Extract phases for the initial test run done by HyperStudy.
    Figure 8. Example of the completed definition run.


  24. Click Next.
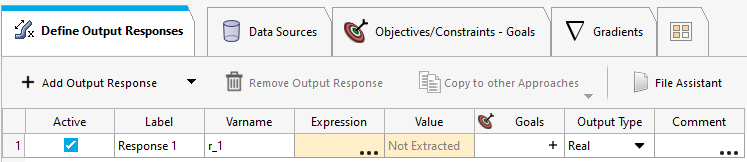
  25. Select Add Output Response.
    An output response is added with the Expression field highlighted.


  26. Select the Expression field.
    The Expression Builder:Response1(r1) dialog is shown.


    Note: The Data Sources m1_ds_1 and m1_ds2 is added from the POSTFEKO graph.
  27. In the Expression field, enter max(m1_ds_1) and click OK.
  28. Under Goals click to add an optimisation goal.
    The following dialog is displayed.
    Figure 9. Example adding an optimisation goal.


  29. Set the goal Type to Minimize and click OK.
  30. Click Evaluate to extract the value from the output file.
    Figure 10. Example selecting the Evaluate button.


    HyperStudy is now configured to understand which model to use, which variables are available for modification and how to process the output.
  31. Right-click on the defined study in the Explorer tab and click Add.
    Figure 11. The Add dialog and selecting an optimisation approach.


  32. Under Select Type, select Optimization.
  33. In the Definition from: drop-down list, select Setup and click OK
    The optimisation approach is created in the Explorer tab
    Figure 12. Example of the Optimisation 1 approach created.


  34. Click Optimization 1 > Specifications, and select the Adaptive Response Surface Method as the optimiser.
    Figure 13. Selecting the Adaptive Response Surface Method.


  35. Click Apply and click Next.
    Figure 14. Example selecting the Apply button.


  36. Click Evaluate Tasks.
    Figure 15. Example selecting the Evaluate Tasks button.


    Each of the input variables is altered randomly, and its effect on the response analysed.
    Figure 16. Typical progress data for an ARSM optimisation.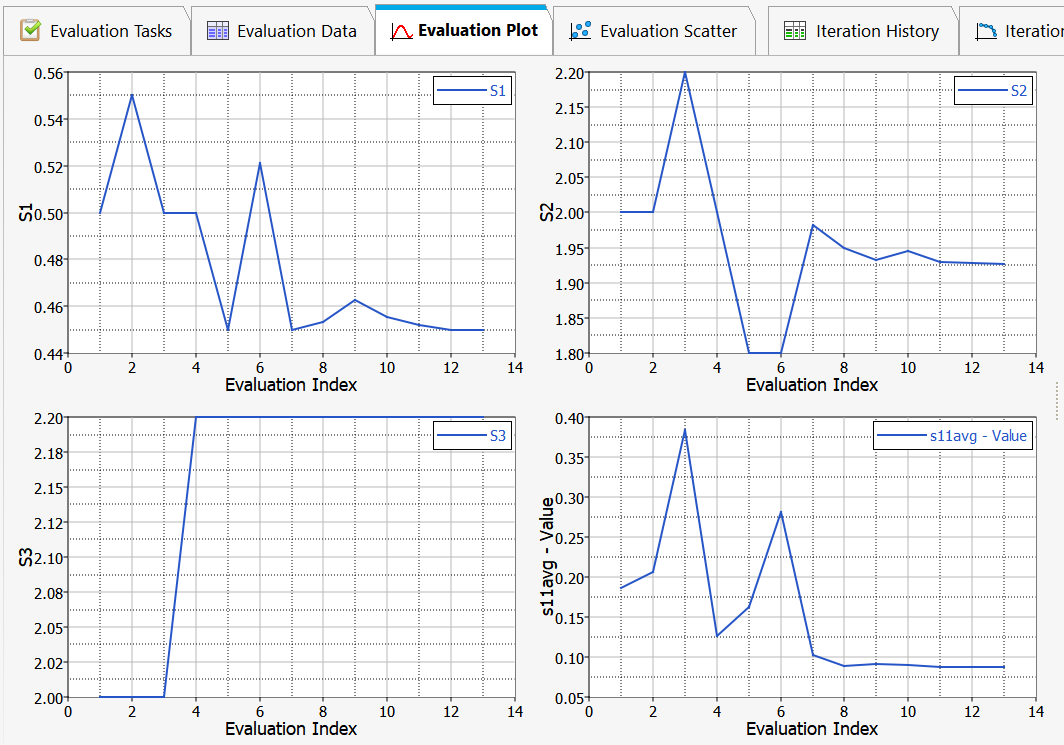


  37. Click Iteration History tab and look for the row highlighted in green.
    The optimum values are as follows:
    • S1 = 0.4500000
    • S2 = 1.9254786
    • S3 = 2.2000000