Description of the Indoor Estimation Models

Obtain coverage inside buildings for the planning of mobile radio networks using different models for indoor coverage prediction.

Different models for the estimation of the indoor coverage were developed. These models allow to compute an estimation of the indoor coverage from an area-wide urban prediction.

The term estimation should rather be used since the prediction is computed without consideration of the inner structure of the buildings. This naturally limits the accuracy of the prediction.

Models Based On the Penetration Loss

Two models are available that are based on the penetration loss (which is equal to the material parameter transmission loss).

The first model, which is an empirical model, computes a homogeneous field strength in the inner of a building by averaging the prediction values at the pixels surrounding the building and subtracting the transmission loss.

The second model, which is a semi-deterministic model, considers the angle of the incident rays. If the empirical COST-Walfisch-Ikegami model is used, the angle information is not available and is thus assumed to be 90°. Currently also for the intelligent ray-tracing (IRT), no angle information is available. Subsequently, it leads to a constant penetration loss.

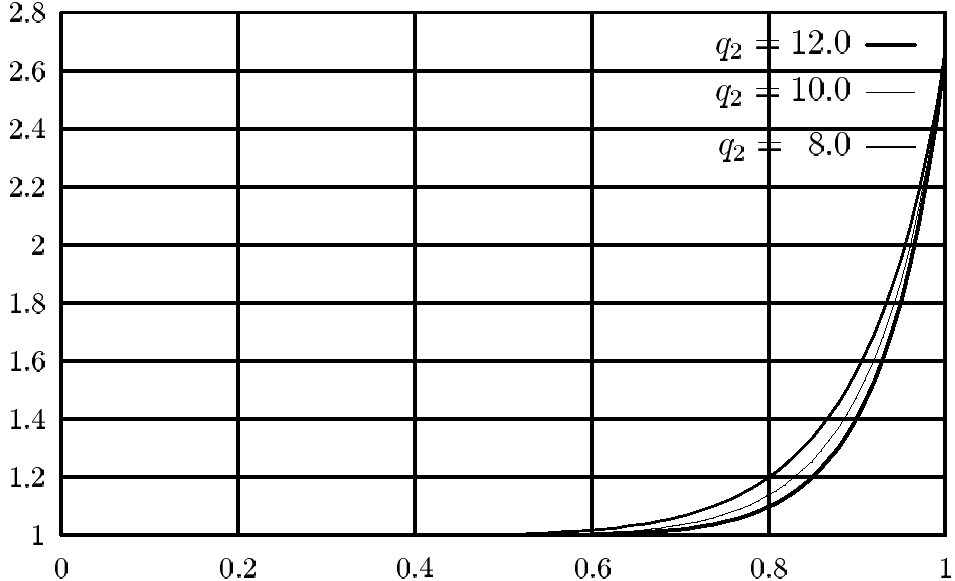
Furthermore, this model can be calibrated using four parameters $q_{1}$ , $q_{2}$ , $q_{3}$ and $q_{4}$ . The following default values should be used: $q_{1} = 1.0$ , $q_{2} = q_{4} = 10.0$ , and $q_{3} = - 0.25$ . The penetration loss $l_{p}$ at arbitrary angles $ϕ$ relative to the penetration loss at $ϕ = 90 °$ is computed using the following equation:

\frac{l_{p}}{l_{p} (φ = 90 °)} = \frac{1 + q_{1} {(\frac{φ}{90 °})}^{q 2}}{1 + q_{3} {(\frac{φ}{90 °})}^{q 4}}

Figure 1 shows the penetration loss $l_{p}$ dependency on the incident angle. For $q_{1}$ , $q_{3}$ and $q_{4}$ the default values were chosen.

Figure 1. Dependency on the penetration loss on the incident angle.

Different Heights

It is required at times to compute the indoor estimation at different heights. This is possible with an extension to the two described models.

Empirical Model

In the empirical model, an additional floor loss $l_{s}$ (in dB/m) must be specified.

The field strength in height $h_{2}$ is then computed from the originally computed field strength on the height $h_{1}$ , which is the same height as for the urban preprocessing:

E (h_{2}) = E (h_{1}) + (h_{2} - h_{1}) l_{s}

This naturally leads to higher field levels on higher floors. A limitation to the field strength computed outside the buildings is included.

Semi-Deterministic Model

In this model, the pixels surrounding the buildings are computed with the urban prediction at the corresponding height. If the standard ray-tracing is used, then the incident angle of the rays are correctly considered.